Cách tính khoản phải trả, tiền gốc, tiền lãi bằng hàm PMT, PPMT, IPMT trong Excel

Nếu bạn đang có một tập hợp gồm vô vàn bảng danh sách cảc khoản vay cần tính khoản phải trả, tiền gốc, tiền lãi theo rất nhiều thời hạn cùng lãi suất khác nhau, mà chỉ sử dụng thao tác thủ công sẽ rất dễ khiến bạn bị nhầm lẫn, xuất hiện sai sót.

Trong bài này Gitiho sẽ giới thiệu cho bạn giải pháp nhanh và dễ nhất để bạn giải quyết vấn đề này. Không chỉ áp dụng cho các khoản vay, còn dùng được cho các khoản đầu tư lẫn tiền gửi ngân hàng,...Để biết cách tính như nào ta cùng xem ví dụ minh họa chi tiết bên dưới nhé.

Hàm PMT, IPMT, PPMT là gì?

PMT, IPMT, PPMT là một trong số những hàm tài chính thường được sử dụng nhất và có vai trò quan trọng trong tính toán liên quan tài chính.

Chúng ta có một ví dụ điển hình cho tác dụng của hàm PMT là tính số tiền vay phải trả dựa trên các khoản thanh toán cố định và lãi suất không đổi. Trong bài này Gitiho sẽ hướng dẫn chi tiết cho bạn qua các ví dụ dễ hiểu và dễ làm theo.

Ví dụ về dùng hàm PMT

Cùng xem xét một khoản vay với lãi suất hàng năm là 6%, thời hạn 20 năm. Giá trị hiện tại là 150.000 đô la (số tiền đã vay) và giá trị tương lai là 0 (nghĩa là khi đã trả hết khoản vay).

1. Dùng hàm PMT tính khoản phải trả hàng năm.

Ta điền công thức sau vào ô trống cần trả kết quả.

=PMT(B2,C2,D2,E2)

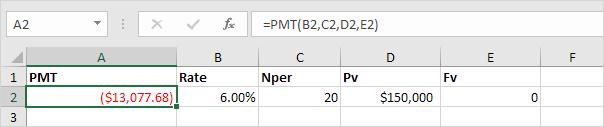
Chú ý: Nếu như đối số thứ 5 trong công thức bị bỏ qua thì có nghĩa là các khoản thanh toán đến hạn vào cuối kỳ. Chúng ta cần trả khoản vay là 150 nghìn đô la (giá trị dương) và thanh toán hàng năm một khoản là 13,077.68 đô la (giá trị âm).

2. Dùng hàm PMT tính khoản phải trả hàng quý.

Ta vẫn điền công thức tương tự vào ô trống cần trả kết quả.

=PMT(B2,C2,D2,E2)

Tuy nhiên điểm khác biệt là ta đã thay đổi lãi suất xuống còn 1,50% và Nper là 80. Giống như trong hình dưới đây.

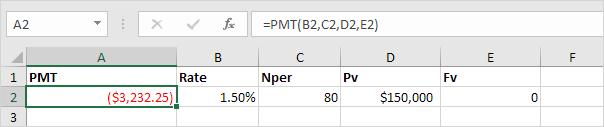
Chú ý:

• Để tính khoản phải trả hàng quý, ta cần chia lãi suất năm thành 4 phần tức là 6% / 4 = 1,5% là lãi suất hàng quý.
• Tổng số kỳ Nper là 20*4=80.

3. Dùng hàm PMT tính khoản phải trả hàng tháng.

Tương tự như trên ta vẫn dùng công thức =PMT(B2,C2,D2,E2). Tuy nhiên cần thay đổi thông số của lãi suất hàng năm và Nper. Như hình minh họa dưới đây.

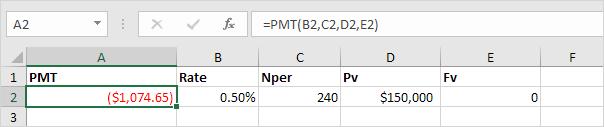
Chú ý:

• Để tính khoản phải trả hàng tháng, ta sẽ sử dụng lãi suất là 6% / 12 = 0,5%.
• Tổng số kỳ là 20*12=240 để điền vào Nper.

Do đó ta có thể thấy được vai trò của hàm PMT cực kỳ hữu ích và giúp ta tiết kiệm được rất nhiều thời gian. Để có thể biết thêm cách sử dụng chi tiết của các hàm này và 150+ hàm Excel, bạn có thể tham khảo khóa học Tuyệt đỉnh Excel của Gitiho:

4. Dùng hàm PMT tính khoản tiền gửi hàng năm.

Với hàm PMT, ta hoàn toàn có thể giải quyết vấn đề sau một cách dễ dàng: Có một khoản đầu tư có lãi suất hàng năm là 8% và giá trị hiện tại là 0. Ta nên gửi bao nhiêu tiền vào mỗi cuối năm để có 1,448.66 đô la trong tài khoản trong 10 năm?

Ta xem hình minh họa dưới đây.

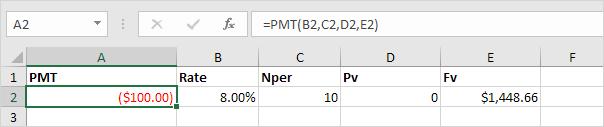
Giải thích: Trong thời gian 10 năm, bạn phải trả 10*100=1000 đô la và bạn sẽ nhận được 1,448.66 đô la sau 10 năm. Lãi suất càng cao, tiền của bạn lại càng tăng nhanh và nhiều.

5. Dùng hàm PMT tính khoản tiền rút hàng tháng.

Cùng xem xét một vấn đề rất phổ biến như sau: ta có một khoản tiền có lãi suất hàng năm là 6% và giá trị hiện tại của nó là 83,748.46 đô la (có thể sử dụng). Ta có thể rút được bao nhiêu tiền vào cuối mỗi tháng trong 20 năm tới?

Ta xem hình minh họa bên dưới đây.

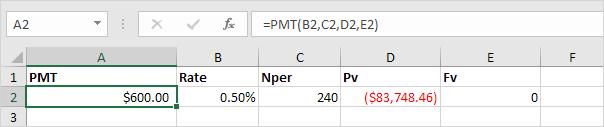
Giải thích: 

• Ta sẽ trả một lần là 83,748.46 đô la.
• Nhận được 240*600=144.000 đô la trong tương lai.
• Đây là một ví dụ cho thấy tiền có thể sinh sôi theo thời gian.

Ví dụ về dùng hàm PPMT và IPMT

Cùng xem xét một khoản vay với lãi suất hàng năm là 5% có thời hạn 2 năm và giá trị hiện tại là 20 nghìn đô la (tức là số tiền đã vay).

1. Dùng hàm PMT để tính số tiền phải trả hàng tháng.

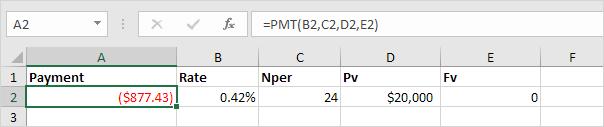
Chú ý: Để tính số tiền phải trả hàng tháng ta cần chỉnh lãi suất thành 5% / 12 = 0,42% và tổng số kỳ là 2*12=24 ghi vào Nper.

2. Dùng hàm PPMT để tính tiền gốc .

Ta xem hình dưới đây. Điền công thức vào ô trống cần trả kết quả.

=PPMT(B2,5C2,D2,E2)

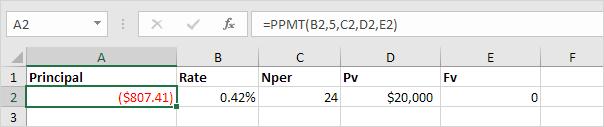
Giải thích: Hàm PPMT ở trên tính cho ta số tiền gốc phải trả trong lần thanh toán thứ 5.

3. Dùng hàm IPMT để tính tiền lãi.

Hàm IPMT trong Excel sẽ giúp ta tính được phần lãi phải trả. Trong công thức đối số thứ 2 xác định số lần trả.

=IPMT(B2,5,C2,D2,E2)

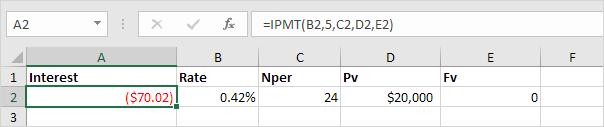
Giải thích: Hàm IPMT trong công thức trên giúp ta tính phần lãi của lần thanh toán thứ 5.

4. Tạo lịch trả dần cho khoản vay.

Cần phải mất 24 tháng để trả hết khoản vay này. Ta có thể tạo một lịch chi trả dần cho khoản vay như hình bên dưới để thấy rõ phần gốc tăng và phần lãi giảm theo từng lần thanh toán.

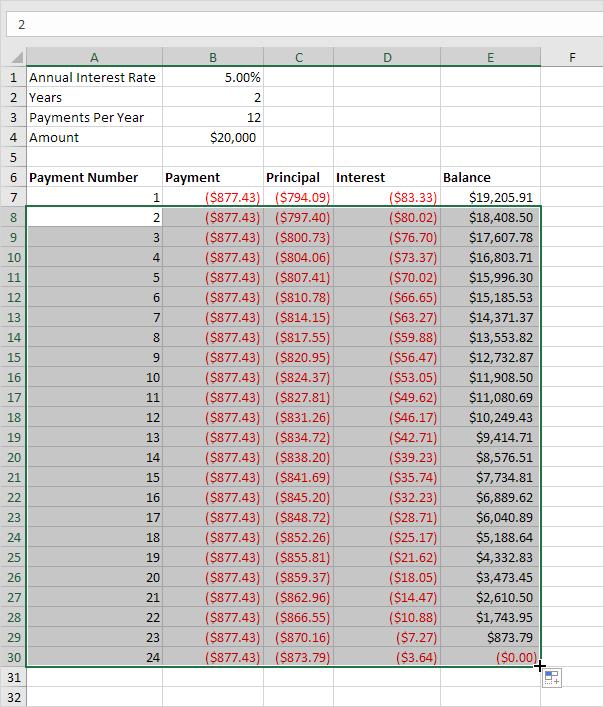
Chú ý: phần gốc lẫn phần lãi sẽ luôn cộng dồn vào số tiền phải trả.

Như vậy chúng ta đã biết được tác dụng và cách sử dụng của các hàm tài chính PMT, PPMT và IPMT rồi.

Kết luận

Trên đây là cách tính khoản phải trả tiền gốc, tiền lãi bằng hàm PMT, PPMT, IPMT trong Excel. 

Gitiho chúc bạn thành công!