Cùng tìm hiểu hàm IRR và cách sử dụng của hàm IRR trong thực tế
Nói ngắn gọn thì hàm IRR là một loại hàm để đánh giá hiệu quả của một dự án hoặc một phương án đầu tư cho các tập đoàn, công ty hoặc nhà đầu tư. Với sự cụ thể trong công dụng như vậy thì không khó để thấy rằng hàm IRR không được nhiều người sử dụng biết tới. Trong bài viết này, Gitiho.com sẽ cùng các bạn thì hiểu rõ hơn về loại hàm IRR và cách sử dụng của hàm này trong thực tế.
Ý nghĩa của hàm IRR
IRR hay "Internal Rate of Return" có thể dịch sang tiếng Việt nghĩa là "tỷ suất hoàn vốn nội bộ".
Để đi sâu vào hàm này, ta có một số điều kiện khác như tỷ suất chiết khấu mà tại đó NPV = 0 tức dự án đó không còn bị lỗ. Hay có một cách hiểu khác là tốc độ tăng trưởng mà dự án đó tạo ra. Bên cạnh đó, IRR có thể ước lượng được tỷ suất chi phí cao nhất mà dự án đó có thể chấp nhận được để tới được điểm hoà vốn, tức NPV=0 tại một thời điểm nhất định. Vì vậy mà IRR được dùng để đo lường mức độ rủi ro trong tương lai.
Để xác định dự án ta đang hướng đến có lãi hay không thì ta cần xét IRR lớn hơn tỷ suất chiết khấu và IRR càng lớn càng tốt.
Cú pháp của hàm IRR
Hàm IRR có cú pháp trong Excle như sau
=IRR(values, guess)
Trong đó những thành phần trong hàm có nghĩa như như sau:
- Values là giá trị nhập để tính toán, bao gồm:
+ Giá trị đầu tư ban đầu (số âm)
+ Những giá trị theo sau là lợi nhuận hàng năm của dự án (sắp xếp theo trình tự thời gian)
- Guess: Tỉ lệ % ước lượng gần với kết quả IRR (mặc định là 10%). Ngoài ra nếu như kết quả tính ra lỗi #NUM! thì ta cũng có thể thử thay đổi giá trị Guess để xem hàm IRR có ra kết quả hay không
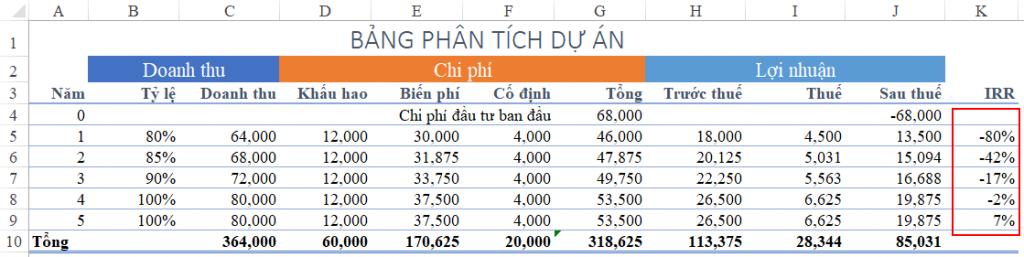
Nhìn vào bảng tính này ta thấy được những điều sau:
- Chi phí ban đầu bỏ ra là 68.000, vậy nên khi xét trong hàm IRR thì giá trị này là dấu âm
- Khi xét IRR, lợi nhuận hàng năm trong dự án là số dương vì đây là khoản tiền được thu về
Dựa vào bảng tính ta có:
- IRR năm đầu tiên: =IRR(J4:J5) = -80%
- IRR bắt đầu từ năm thứ hai: =IRR(J4:J6)= -42%
- IRR năm ba: =IRR(J4:J7)= -17%
- IRR năm tư: =IRR(J4:J8)= -2%
- IRR năm thứ năm: =IRR(J4:J9)= 7%
=> Vậy sau 5 năm thì dự án này sẽ mang về doanh thu
Tuy nhiên nếu như lãi suất chiết khấu (chi phí sử dụng vốn) với tỉ lệ 10% thì sau 5 năm IRR vẫn không có được con số kỳ vọng cho các nhà đầu tư. Thế nên trong thời điểm 5 năm như trên thì dự án này không khả thi vì NPV < 0. Vậy nên để xét tính khả thi của một dự án tiềm năng thì ngoài việc xét yếu tố IRR thì còn phải xét cả NPV.
Vậy nên giới hạn của hàm IRR chỉ sử dụng được các kỳ tính toán khác nhau.
Mong rằng qua bài viết này, Gitiho.com đã đem lại cho các bạn thêm một loại hàm có tính ứng dụng tương đối cao để sử dụng trước khi dành tiền đầu tư vào các dự án tiềm năng.
Khóa học phù hợp với bất kỳ ai đang muốn tìm hiểu lại Excel từ con số 0. Giáo án được Gitiho cùng giảng viên thiết kế phù hợp với công việc thực tế tại doanh nghiệp, bài tập thực hành xuyên suốt khóa kèm đáp án và hướng dẫn giải chi tiết. Tham khảo ngay bên dưới!
Giấy chứng nhận Đăng ký doanh nghiệp số: 0109077145, cấp bởi Sở kế hoạch và đầu tư TP. Hà Nội
Giấy phép mạng xã hội số: 588, cấp bởi Bộ thông tin và truyền thông