Hướng dẫn tạo biểu đồ hộp Box and Whisker Plot trong Excel

Biểu đồ hộp có tên tiếng anh là Box and Whisker Plot. Đây là dạng biểu đồ biểu diễn sự phân bố các thành phần, trong đó thể hiện được giá trị nhỏ nhất, giá trị lớn nhất của tập dữ liệu cũng như giá trị một phần tư đầu tiên, phần tư ở thứ hai, thứ ba của tập dữ liệu. Trong bài viết này chúng ta cùng tìm hiểu cách vẽ biểu đồ hộp (biểu đồ box and whisker) trong Excel nhé.

Tạo biểu đồ hộp đơn giản trên Excel

Để vẽ được biểu đồ hộp, trước hết bạn sẽ cần có 1 tập dữ liệu. Sau đó chúng ta chỉ cần thực hiện một số thao tác chọn mẫu biểu đồ trên Excel là có thể tạo ra ngay mẫu biểu đồ này. Các bước thực hiện như sau:

Bước 1. Trong ví dụ này ta sẽ chọn dải ô A1:A7 là nơi có sẵn tập dữ liệu đã chuẩn bị trước:

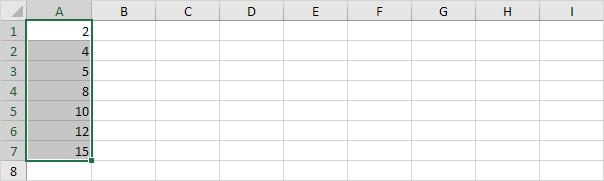
Chú ý: Bạn không cần sử dụng tính năng sắp xếp dữ liệu từ nhỏ nhất tới lớn nhất nhưng thao tác này giúp ta phân tích rỗ hơn về biểu đồ hộp.

Bước 2. Trên thanh công cụ của Excel chọn thẻ Insert  > nhấn chọn nhóm tiếp mục Chart > chọn tiếp biểu tượng Statistic Chart như hình bên dưới

Bước 3. Nhấn chọn biểu đồ trong phần Box and Whisker.

Lúc này ta thu được biểu đồ như hình dưới đây.

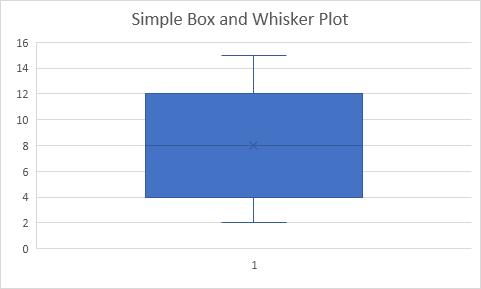
Giải thích các thành phần trong biểu đồ:

• Dòng giữa của hộp thể hiện số trung vị hoặc số ở giữa (8).
• Dấu x trong hộp cho biết giá trị trung bình (cũng là giá trị 8 trong ví dụ này).
• Trung vị chia tập dữ liệu thành 2 nửa. Nửa dưới 2,4,5 và nửa trên 10,12,15.
• Dòng dưới cùng của hộp biểu thị giá trị trung bình của nửa dưới hoặc phần tư thứ nhất (4).
• Dòng trên cùng của hộp biểu thị giá trị trung bình của nửa trên hoặc phần tư thứ ba (12).
• Đường thẳng đứng hay còn gọi là Râu kéo dài từ hai đầu hộp giữa gái trị nhỏ nhất (2) và giá trị lớn nhất (15).

Giá trị ngoại lai

Giá trị ngoại lai, cá biệt (Outliers) là những giá trị nằm ngoài khoảng các giá trị liền kề. Ta cùng xem chi tiết ví dụ minh họa dưới đây.

Bước 1. Trong ví dụ này ta chọn dải ô A1:A11.

Chú ý:

• Trung vị và số nằm giữa (8) chia dữ liệu thành 2 nửa gồm (1, 2, 2, 4, 5) và (10, 12, 15, 18, 35).
• Phần tư thứ nhất Q1 là trung vị của nửa đầu tiên. Q1 = 2. 
• Phần tư thứ ba Q3 là trung vị của nửa thứ hai. Q3 = 15.

Bước 2. Trên tab Insert, chọn nhóm Charts, nhấn chọn biểu tượng Statistic Chart.

Bước 3. Nhấn chọn Box and Whisker.

Lúc này ta thu được biểu đồ như hình bên dưới.

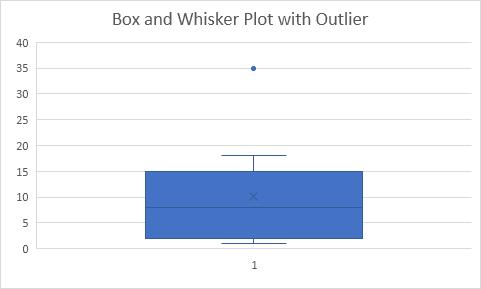
Giải thích:

• Phạm vi liên phần tư (IQR) được xác định là khoảng cách giữa phần tư thứ nhất và phần tư thứ ba. 
• Trong ví dụ này IQR = Q3 - Q1 = 15 - 2 = 13.
• Một điểm dữ liệu ngoại lệ khi nó quá 1.5 lần IQR bên dưới phần tư thứ nhất (Q1 - 1.5 * IQR = 2 - 1.5 * 13 = -17.5) hoặc gấp 1.5 lần IQR trên phần tư thứ ba (Q3 + 1.5 * IQR = 15 + 1.5 * 13 = 34.5).
• Do đó, trong ví dụ này thì 35 được coi là giá trị ngoại lai.
• Ta thấy được kết quả là Râu trên cùng của hộp mở rộng đến giá trị lớn nhất là 18.

Bước 4. Thay đổi điểm dữ liệu cuối cùng thành 34.

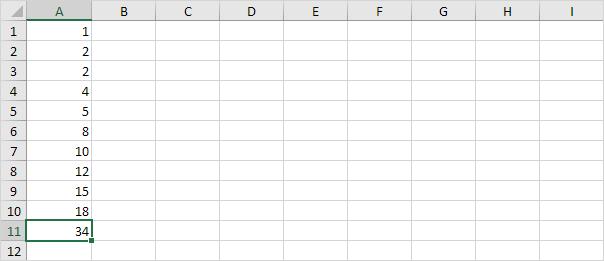
Ta thu được kết quả như hình dưới.

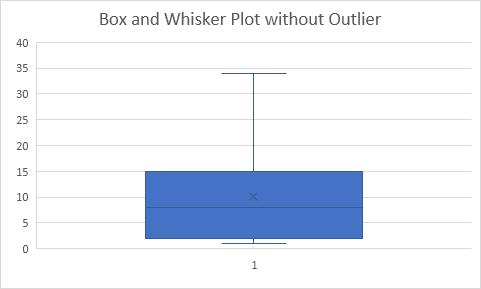
Giải thích: Tất cả các điểm dữ liệu nằm giữa -17.5 và 34.4. Như kết quả trên ta thấy râu biểu đồ nối liền giữa giá trị nhỏ nhất là 2 và giá trị lớn nhất là 34.

Ngoài ra, để sử dụng Excel vẽ biểu đồ thành thạo và áp dụng vào lập báo cáo một cách chuyên nghiệp, bạn có thể tham khảo khóa học Excel nâng cao của Gitiho:

Phép tính trong biểu đồ hộp

Hầu như ta không thể dễ dàng xác định được phần tư thứ nhất và thứ ba nếu không thực hiện các phép tính.

Bước 1. Trong ví dụ này ta chọn 7 số của các điểm dữ liệu bên dưới.

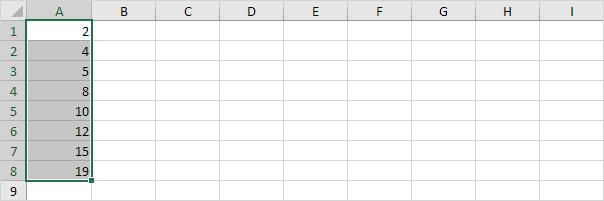
Bước 2. Trên tab Insert, chọn nhóm Charts, nhấn chọn biểu tượng Statistic Chart.

Bước 3. Nhấn chọn Box and Whisker.

Lúc này ta thu được biểu đồ như hình bên dưới.

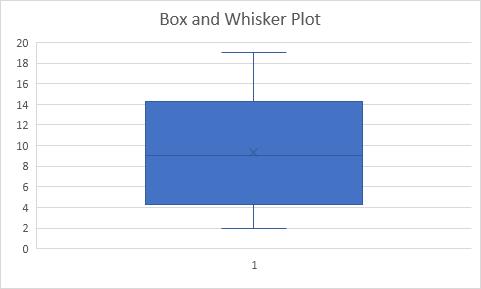
Giải thích:

• Excel sửa dụng hàm QUARTILE.EXC để tính phần tư thứ nhất Q1, phần tư thứ 2 Q2 và phần tư thứ 3 Q3. 
• Hàm này tự thêm vào giữa hai giá trị để tính một phần tư. Trong ví dụ này n = 8 (số điểm dữ liệu).

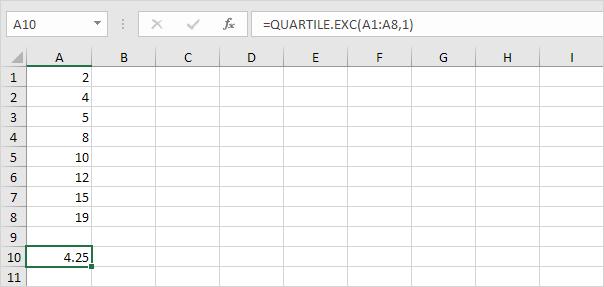
Bước 4. Q1 = 1/4*(n+1)th value = 1/4*(8+1)th value = 2 1/4th value = 4 + 1/4 * (5-4) = 4 1/4.

Ta có thể xác minh con số này bằng cách sử dụng hàm QUARTILE.EXC hoặc xem trên biểu đồ hộp.

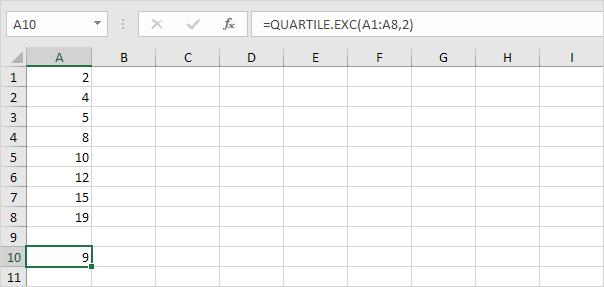
Bước 5. Q2 = 1/2*(n+1)th value = 1/2*(8+1)th value = 4 1/2th value = 8 + 1/2 * (10-8) = 9.

Trong trường hợp này, giá trị trung vị là trung bình của hai số ở giữa.

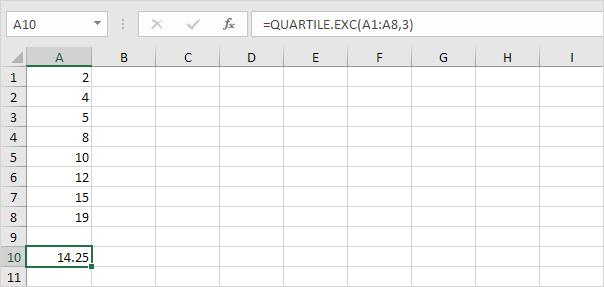
Bước 6. Q3 = 3/4*(n+1)th value = 3/4*(8+1)th value = 6 3/4th value = 12 + 3/4 * (15-12) = 14 1/4. Tương tự như trên ta có thể xác minh con số này bằng cách sử dụng hàm QUARTILE.EXC hoặc nhìn trên biểu đồ hộp.

Như vậy ta đã nắm được kiến thức cơ bản và cách tạo biểu đồ hộp trên Excel rồi. Hy vọng bạn sẽ có thể ứng dụng được kiến thức này vào công việc.

Chúc bạn thành công!