Cách tính tổng lũy kế bằng công thức mảng và hàm MMULT trong Google Sheets

Running total hay còn gọi là tổng lũy kế được tính bằng cách cộng dồn liên tiếp các giá trị. Trong bài viết này, chúng ta sẽ tìm hiểu các tính tổng lũy kế, sử dụng phương pháp chuẩn và phương pháp công thức mảng.

Chúng ta cũng sẽ đề cập đến chủ đề về phép nhân ma trận, sử dụng một công thức khá thử thách là MMULT trong Google Sheets.

Trong các ví dụng bên dưới, chúng ta sẽ sử dụng tập dữ liệu này:

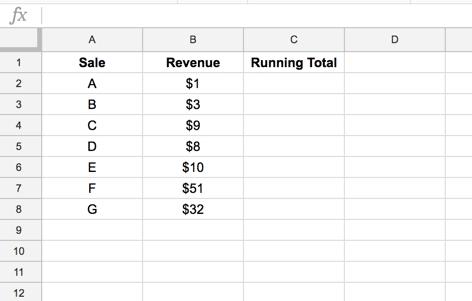
Chúng ta sẽ tính tổng lũy kế trong cột C Running total.

Cách tính tổng lũy kế bằng công thức cơ bản

Hãy bắt đầu với phương pháp cơ bản nhất, sử dụng công thức chuẩn (không phải Mảng) mà sau đó chúng ta chỉ cần kéo công thức này xuống các cột bên dưới.

Với tập dữ liệu ở trên,  chúng ta nắt đầu tính tổng lũy kế ở ô C2, với công thức sau:

= B2

Công thức này chỉ trả về giá trị đầu tiên của chúng ta, đó là giá trị duy nhất mà chúng ta có ở giai đoạn này.

Đối với giá trị thứ hai trở đi, chúng ta có thể sử dụng cùng một công thức chuẩn, chỉ cần thêm giá trị mới vào tổng  từ dòng trên:

= B3 + C2

Sau đó, công thức này có thể được kéo xuống theo yêu cầu để đưa ra tổng số lũy kế:

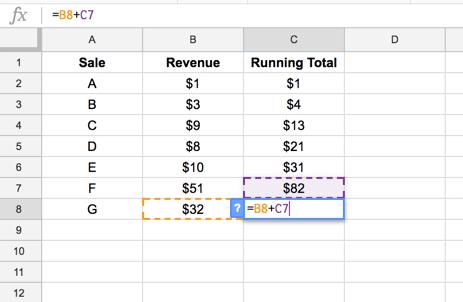
Nếu các mục mới được thêm vào tập dữ liệu, công thức này sẽ cần phải tiếp tục được kéo xuống. Hoặc bạn có thể điền trước các ô trong cột bằng cách kéo đến cuối Trang tính của mình và gói trong câu lệnh IF để ẩn trên các hàng trống, như sau:

=IF(ISBLANK(B3),"", B3 + C2)
 

Nhược điểm chính của công thức này là bạn cần phải điền vào toàn bộ cột với một công thức mới cho mỗi hàng.

Nếu chúng ta viết một công thức duy nhất ở đầu cột để tính tổng lũy kế cho toàn bộ ô còn lại thì sao? Nhưng khi đến với công thức mảng tuyệt vờ đó, bạn hãy thử khám phá một chút về phép nhân ma trận bên dưới.

Phép nhân ma trận trong Google Sheets

Nội dung của phần nãy sẽ liên quan đến hàm MMULT, được định nghĩa như sau:

Tích AB của ma trận A = (aij) và B = (bhk) is ) được xác định nếu và chỉ khi số cột của A bằng số hàng của B.

Nói cách khác nếu A có dạng (m, n) thì B phải có dạng (n, p), để hàm này hoạt động. Ma trận kết quả sẽ có dạng (m, p). Mỗi mục nhập trong ma trận mới được xác định bởi quy tắc

(i, k) entry of AB = ith row of A * kth column of B

Công thức MMULT thực hiện phép nhân ma trận này cho chúng ta. Nó nhận ma trận A và B làm đối số =MMULT(A,B) và xuất ra sản phẩm là ma trận AB.

Bây giờ, bạn hãy gác mấy định nghĩa toán học này sang một bên, quay trở lại nền tảng Google sheets vô cùng thân thuộc của chúng ta.

Tính tổng lũy kế bằng công thức mảng

Sau khi bạn đã tìm hiểu xong cách thực hiện phép nhân ma trận, hãy sử dụng điều đó trong ví dụ bên dưới với hàm MMULT .

Hãy lập chiến lược trước khi đi sâu vào các công thức và lưu ý rằng:

1.  Ma trận hàng đơn, 1 x, nhân với ma trận cột đơn có kích thước tương thích, X-x 1, sẽ dẫn đến ma trận 1 x 1, tức là một giá trị duy nhất.
2. Tiến thêm một bước nữa, nếu ma trận hàng là {a,b,c} và ma trận cột {x;y;z}, thì tích sẽ là ax + by + cz một giá trị duy nhất, là tổng của các phần tử được nhân với nhau.
3. Vì vậy, nếu chúng ta có thể lấy các giá trị từ phạm vi của chúng ta trong cột B thành một định dạng hàng và nhân chúng với một vectơ cột, chúng ta sẽ có thể cộng chúng lại!
4. Mẹo ở đây là tạo ma trận 1 chỉ có các giá trị "đúng" trong mỗi hàng, vì vậy đối với hàng 1, nó chỉ nên có giá trị đầu tiên, đối với hàng 2, nó phải có hai giá trị đầu tiên, đối với hàng 3 là giá trị đầu tiên. ba,... Tức là chỉ các giá trị hiện tại hoặc trước đó trong mỗi hàng của ma trận của chúng ta.
5. Ma trận 2 chỉ đơn giản cho phép phép nhân xảy ra, để các giá trị có thể được thêm vào. Vì vậy,  một vectơ của 1 là đủ.

Quay lại vấn đề hiện tại, bằng cách sử dụng tập dữ liệu được chia sẻ ở đầu bài này, hãy bắt đầu bằng cách xây dựng hai ma trận với hàm MMULT của chúng ta. Tôi khuyên bạn nên hạn chế phạm vi thành B2:B10, để giữ cho các phép tính có thể quản lý được trong khi chúng ta phân tích công thức. Khi công thức của chúng ta đã hoạt động, bạn có thể mở phạm vi tới B2:B.

Bắt đầu với công thức này trong ô E2:

=ArrayFormula(ROW(B2:B10))

Công thức này chỉ đơn giản là cung cấp cho chúng ta một vectơ cột của các số từ 2 đến 10, tức là {2;3;4;5;6;7;8;9;10}

Thêm công thức này vào ô F1:

=ArrayFormula(TRANSPOSE(ROW(B2:B10)))

Công thức này chỉ đơn giản là chuyển vectơ cột ở trên thành một vectơ hàng gồm các số, tức là {2,3,4,5,6,7,8,9,10}

Bây giờ, hãy tạo ma trận 9 x 9, bằng cách so sánh hai vectơ này và ghi lại xem giá trị từ vectơ cột nhỏ hơn hoặc bằng giá trị từ vectơ hàng hay không, bằng cách sử dụng công thức:

=ArrayFormula(ROW(B2:B10) <= TRANSPOSE(ROW(B2:B10)))

Bây giờ chúng ta sẽ có đầu ra như sau:

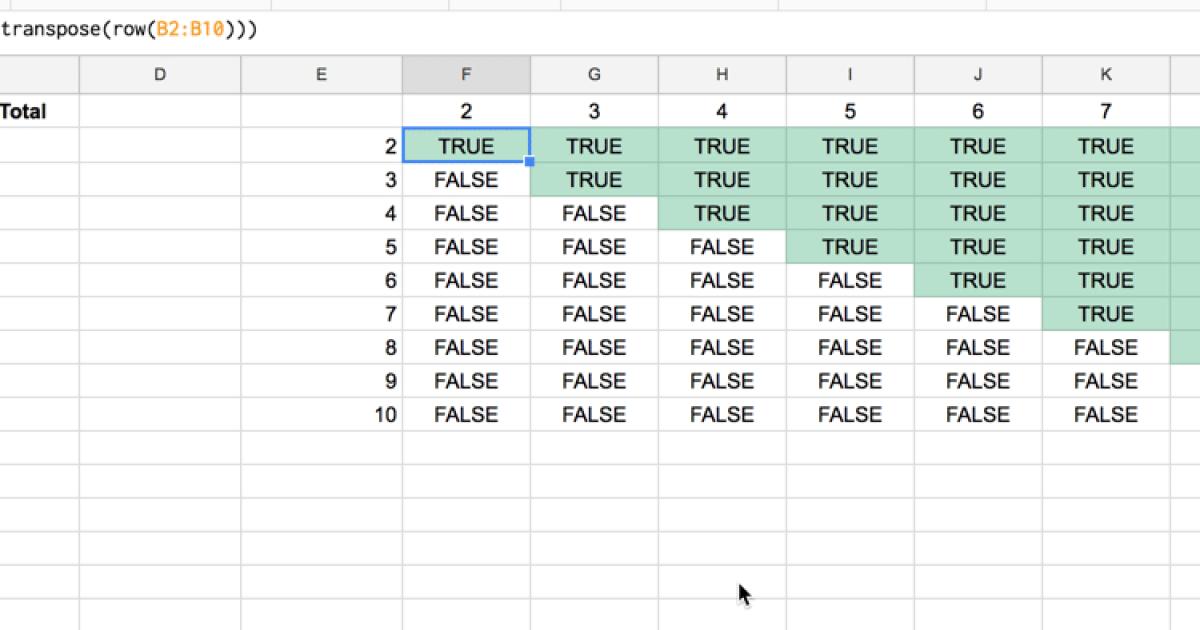
Ma trận vectơ hàng và cột này cho kết quả là TRUE khi có giá trị vectơ cột nhỏ hơn hoặc bằng giá trị vectơ hàng và ngược lại là false.

Nhân giá trị này với phạm vi dữ liệu gốc, B2: B10, biến các giá trị TRUE thành số và giá trị FALSE thành số không:

=ArrayFormula((ROW(B2:B10) <= TRANSPOSE(ROW(B2:B10)))*B2:B10)

Chúng ta sẽ áp dụng một hàm chuyển vị TRANSPOSE, để lật dữ liệu sang hướng chính xác

=ArrayFormula(TRANSPOSE((ROW(B2:B10) <= TRANSPOSE(ROW(B2:B10)))*B2:B10))

Dữ liệu B2: B10 hiện đang ở vị trí 9 x 9, bắt đầu chính xác từ hàng tương ứng của chúng (vì vậy giá trị trong B2 bắt đầu từ hàng 2, giá trị trong B3 bắt đầu ở hàng 3,...), như thể hiện trong hình ảnh này:

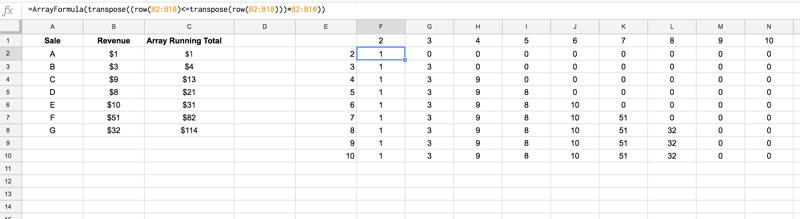
Vậy là ma trận 1 đã sẵn sàng cho công thức MMULT.

Hãy băt đấu xây dựng ma trận 2. Rất may là ma trận đơn giản hơn một chút so với ma trận 1:

=ArrayFormula(SIGN(B2:B10))

Công thức này để tạo ma trận 9 x 1 hoặc vectơ cột, trong đó bất kỳ số dương nào trong phạm vi B2: B10 trả về 1 và các ô trống trả về 0, vì vậy kết quả cuối cùng là vectơ cột của chúng ta là {1;1;1;1;1;1;1;0;0}

Đặt cả hai thứ này vào hàm MMULT và xem điều kỳ diệu xảy ra:

=ArrayFormula(MMULT(TRANSPOSE((ROW(B2:B10)

<= TRANSPOSE(ROW(B2:B10)))*B2:B10),SIGN(B2:B10)))

Từ phép nhân ma trận, ma trận 9 x 9 nhân với ma trận 9 x 1 của chúng ta sẽ tạo ra ma trận 9 x 1 mới.

Mỗi phần tử trong hàng đầu tiên của ma trận 1 được nhân với các giá trị cột trong ma trận 2 và được cộng lại với nhau, trông giống như sau:

Hàng đầu tiên của ma trận 1 là {1,0,0,0,0,0,0,0,0}

Cột đầu tiên của ma trận 2 là {1;1;1;1;1;1;1;0;0}

Do đó giá trị đầu tiên trong ma trận mới là:

1*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*0 + 0*0

= 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0

= 1

(Bạn có thể nhận thấy rằng đây là ma trận 1 x 9 nhân với ma trận 9 x 1, tạo ra ma trận 1 x1, hay đơn giản là một giá trị duy nhất.)

Tương ứng như trên, phép tính cho hàng 2 sẽ là:

1*1 + 3*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*0 + 0*0

= 1 + 3 + 0 + 0 + 0 + 0 + 0 + 0 + 0

= 4

Hàng 3:

1*1 + 3*1 + 9*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*0 + 0*0

= 1 + 3 + 9 + 0 + 0 + 0 + 0 + 0 + 0

= 13

Cứ thế tiếp diễn và đầu ra cuối cùng sẽ là

{1;4;13;21;31;82;114;114;114}

Vì vậy, công thức này cho ra kết quả là tổng lũy kế.

Bước cuối cùng là chỉ hiển thị nó trên các hàng không trống, chúng ta chỉ cần sử dụng hàm logic IF tiêu chuẩn là được.

Ở đây tôi đã sử dụng cấu trúc này để đảm bảo các ô trong phạm bị B2:B10 trống.

IFERROR(1/0)

Vì vậy, công thức của chúng tôi bây giờ là:

=ArrayFormula( IF(B2:B10,MMULT(TRANSPOSE((ROW(B2:B10)<=TRANSPOSE(ROW(B2:B10)))*B2:B10),SIGN(B2:B10)), IFERROR(1/0)))

Công thức trên có thể được khái quát cho toàn bộ cột B, bằng cách loại bỏ tham chiếu 10 hàng khỏi B2: B10.

Công thức của cuối cùng của chúng ta như sau:

=ArrayFormula(IF(B2:B,MMULT(TRANSPOSE((ROW(B2:B)<=TRANSPOSE(ROW(B2:B)))*B2:B),SIGN(B2:B)), IFERROR(1/0)))

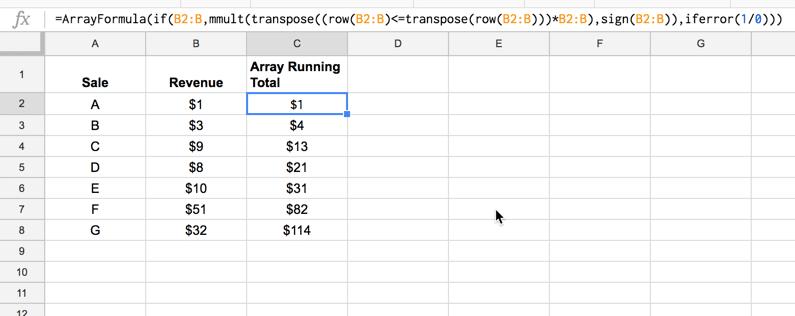
Nếu các hàng dữ liệu mới được thêm vào cột A và B, cột tổng lũy kế sẽ tự động cập nhật.

Công thức mảng có điều kiện tính tổng lũy kế

Bạn có thể tạo một công thức mảng duy nhất để tạo các tổng đang chạy riêng cho từng mục trong Cột A, tối đa 9 mục duy nhất, như được hiển thị trong hình ảnh này:

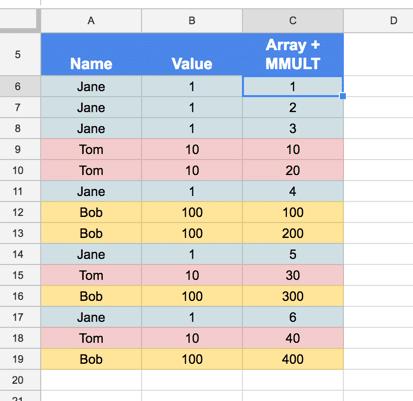
Công thức cho để tạo được bảng tính trên khá phức tạp. Nhưng bạn đừng lo lắng, chúng tôi đã soạn sẵn ngay bên dưới:

=ArrayFormula(query(query(if({transpose(unique(indirect("A6:A"&counta($A$6:$A)+1)))}=$A$6:$A,mmult(transpose((row($B$6:$B)<=transpose(row($B$6:$B)))*$B$6:$B),if({transpose(unique(indirect("A6:A"&counta($A$6:$A)+1)))}=$A$6:$A,1,0)),0),"select "&left(concatenate(transpose("Col"&row(indirect("1:"&countunique($A$6:$A)))&"+")),countunique($A$6:$A)*5-1)&" label "&left(concatenate(transpose("Col"&row(indirect("1:"&countunique($A$6:$A)))&"+")),countunique($A$6:$A)*5-1)&" ''",0),"select * limit "&counta(A6:A)))

Trong phạm vi của bài viết này, tôi không phân tích từng dòng bên trong công thức trên. Tuy nhiên, nếu bạn quan tâm, cách tốt nhất để tiếp cận nó là bóc lại các lớp như ở phần hướng dẫn bên trên, cho đến khi bạn tìm ra công thức trong cùng, và sau đó xây dựng nó trở lại.

Chúng tôi hy vọng qua bài viết này, bạn đã hiểu được cách tính tổng lũy kết bằng công thức cơ bản và công thức mảng, cũng như các sử dụng hàm MMULT để nhân các ma trận trong Google Sheets. Bên cạnh đó, nếu bạn không muốn bỏ lỡ những thủ thuật Tin học văn phòng tuyệt vời nhất, hãy tham gia cùng với Gitiho ngay hôm nay.