Hàm LINEST - Tìm giá trị thống kê cho một đường thẳng trong Excel

Phương trình đường thẳng trong toán học

Phương trình của một đường thẳng nếu có một phạm vi x duy nhất được viết theo cách:

y = mx + b

Trong đó:

• x là biến độc lập;
• y là biến phụ thuộc;
• m là độ dốc (gradient) của đường thẳng;
• b là hằng số, bằng giá trị của y khi x = 0.

Nếu có nhiều phạm vi giá trị x, đường thẳng phù hợp thỏa mãn phương trình sau:

y = m1 x 1 + m2 x 2 + ... + b

Trong đó:

• x là các phạm vi biến độc lập;
• y là biến phụ thuộc;
• m là cấp số nhân hằng số cho mỗi phạm vi x;
• b là một hằng số.

Xem thêm: Hướng dẫn sử dụng Excel giải bài toán lý thuyết thống kê đơn giản

Hàm thống kê LINEST trong Excel

Hướng dẫn sử dụng hàm LINEST trong Excel

Hàm LINEST trong Excel trả về các giá trị thống kê cho một đường bằng phương pháp bình phương nhỏ nhất. Thông qua một tập hợp các giá trị x và y được cung cấp hàm sẽ tính toán đường thẳng phù hợp nhất và trả về một mảng mô tả đường thẳng đó.

Thông tin thống kê cơ bản được trả về là mảng các hằng số mn, mn-1, ..., b cho phương trình: y = m1x1 + m2x2 + ... + b

hoặc, đối với một phạm vi giá trị x duy nhất, hàm trả về các hằng số m và b cho phương trình đường thẳng: y = mx + b.

Cú pháp:

=LINEST(known_y's,[known_x's],[const],[stats])

Trong đó:

- Known_y's (bắt buộc): Mảng các giá trị y đã biết.

- Known_x's (tùy chọn): Mảng của một hoặc nhiều bộ giá trị x đã biết. Nếu known_x's bị bỏ qua thì nó được giả định là 1 mảng có cùng kích thước với known_y's

- Const (tùy chọn): Hằng số 'b' được xử lý trong phương trình 

• TRUE (hoặc bỏ qua): hằng số b được tính toán bình thường;
• FALSE: hằng số b được đặt có giá trị 0 và giá trị m được điều chỉnh để phù hợp với y = mx.

- Stats (tùy chọn): Đối số logic tùy chọn chỉ định xem bạn có muốn hàm trả về thống kê hồi quy bổ sung trên đường thẳng phù hợp nhất hay không.

• TRUE: Trả về thống kê hồi quy bổ sung.
• FALSE (hoặc bị bỏ qua): Không trả về thống kê hồi quy bổ sung.

Bên cạnh đó, ta có thể mô tả các đường thẳng bằng độ dốc và giao cắt y như sau:

• Độ dốc 'm':

Để tìm độ dốc của đường thẳng 'm', ta chọn hai điểm trên đường thẳng đó, ví dụ: (x1,y1) và (x2,y2), từ đó độ dốc bằng (y2 - y1)/(x2 - x1).

Khi có một biến độc lập thì cú pháp LINEST trong trường hợp này là: 

• Giao cắt Y 'b':

Giao cắt y của một đường thẳng là 'b' (giá trị của y tại điểm mà đường thằng cắt trục y

Khi có một biến độc lập thì cú pháp LINEST trong trường hợp này là: 

=INDEX(LINEST(known_y's,known_x's),2)

Lưu ý:

1. Dùng dấu phẩy phân cách giữa các giá trị trong cùng 1 hàng.
2. Dùng dấu chấm phẩy phân cách giữa các hàng với nhau.
   
3. Vì hàm LINEST trả về một mảng giá trị nên nó phải được nhập dưới dạng công thức mảng. Nếu hàm không được nhập dưới dạng công thức mảng, chỉ giá trị 'm' đầu tiên trong mảng thông tin thống kê được tính toán sẽ được hiển thị trong bảng tính của bạn. Bạn có thể xem liệu một hàm đã được nhập dưới dạng công thức mảng hay chưa, vì dấu ngoặc nhọn sẽ được chèn xung quanh công thức, khi nó được xem trong thanh công thức. Hãy xem các ví dụ dưới đây để hiểu hơn bạn nhé!

Ví dụ về hàm LINEST trong Excel

Hãy xem ví dụ và phần giải thích của mình dưới đây để hiểu hơn về hàm LINEST nhé!

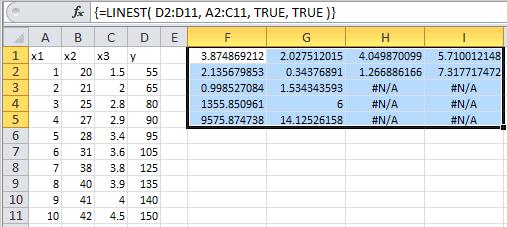
Như bạn có thể thấy trong ảnh trên, các dấu ngoặc nhọn xung quanh hàm cho thấy rằng nó đã được nhập dưới dạng công thức mảng.

Ở đây các phạm vi ô (A2-A11), (B2-B11) và (C2-C11) của bảng tính bên trên chứa ba bộ biến độc lập khác nhau (các giá trị x đã biết) và các ô (D2-D11) của bảng tính chứa các giá trị y đã biết được liên kết. Các ô (F1-I5) của bảng tính hiển thị kết quả của hàm LINEST trong Excel, đã được sử dụng để trả về thông tin thống kê của đường thẳng phù hợp nhất thông qua các điểm này.

Cú pháp hàm LINEST trong trường hợp này là:

= LINEST(D2:D11,A2:C11,TRUE,TRUE)

Theo kết quả trên, ta có:

- Các ô (F1-I1) cung cấp giá trị của các hệ số, m3, m2 và m1 lần lượt là 3,874869212, 2,027512015 và 4,049870099 và điểm giao y 'b' là 5,710012148. Do đó, phương trình đường thẳng đi qua các điểm đã cho là: 

y = 4.049870099 x1 + 2.027512015 x2 + 3.874869212 x3 + 5.710012148

- Các ô còn lại trong phạm vi F1-I5 đưa ra các thống kê bổ sung sau cho đường cong này:

• Giá trị lỗi tiêu chuẩn cho các hệ số m3, m2 và m1 lần lượt là 2,135679853, 0,34376891 và 1,266886166
• Giá trị lỗi tiêu chuẩn cho hằng số b là 7,317717472
• Hệ số xác định là 0,998527084
• Sai số tiêu chuẩn cho ước tính y là 1,534343593
• Thống kê F là 1355.850961
• Số bậc tự do là 6
• Tổng hồi quy của các bình phương là 9575,874738
• Tổng dư của các bình phương là 14.12526158

Những lưu ý khi sử dụng hàm LINEST trong Excel

1. Hàm trả về lỗi #REF!, nếu mảng [known_x's] không cùng độ dài với mảng known_y's.
2. Hàm trả về lỗi #VALUE! nếu bất kỳ giá trị nào trong mảng [known_x's] hoặc known_y's được cung cấp không phải là số hoặc đối số [const] hay [stats] không thể được đánh giá là TRUE hoặc FALSE.

Xem thêm: 25 kỹ năng Excel mà bạn nên biết từ cơ bản, trung cấp đến nâng cao

Kết luận

Hy vọng bài viết này đã giúp bạn hiểu hơn về cách sử dụng hàm LINEST trong Excel để tìm các giá trị thống kê cho một đường thẳng bằng phương pháp bình phương nhỏ nhất. Nếu bạn có bất kỳ câu hỏi nào liên quan đến bài viết này hoặc về bất kỳ chủ đề Excel nào khác, hãy cho chúng mình biết trong phần bình luận bên dưới. Và đừng quên theo dõi chúng mình để xem thêm các bài viết bổ ích khác nhé!