Cách vẽ Tập MandelBrot trong Google Sheet chỉ sử dụng công thức

Tập Mandelbrot được đặt tên theo nhà toán học Benoît Mandelbrot, người đầu tiên đã nghiên cứu và phát triển nó.

Trong bài viết này, Gitiho sẽ hướng dẫn bạn cách vẽ tập Mandelbrot trong Google Sheets, chỉ sử dụng các công thức và công cụ biểu đồ tích hợp sẵn.

Tập Mandelbrot là gì?

Tập Mandelbrot là một nhóm các số đặc biệt với một số đặc tính đáng kinh ngạc, là tập hợp các điểm nằm trong mặt phẳng phức, với biên của nó có dạng fractal.

Tập Mandelbrot là tập các giá trị của số phức c với quỹ đạo bắt đầu từ 0 dướiphép lặp của đa thức bậc hai hệ số phức zn+1 = zn2 + c vẫn bị chặn (đóng trong biên). Có nghĩa là, một số phức c thuộc về tập Mandelbrot, khi bắt đầu với z0 = 0 và áp dụng phép lặp lại, thì giá trị tuyệt đối của zn không bao giờ vượt quá một số xác định (số này phụ thuộc vào c) cho dù n lớn như thế nào. 

Nghe có vẻ phức tạp nhưng chắc chắn bạn gần đã nhìn thấy hình ảnh của tập Mandelbrot trước đây.

Đó là một trong những khái niệm toán học nổi tiếng nhất, cả bên trong lẫn bên ngoài lĩnh vực toán học, được đặt theo tên nhà toán học người Pháp, Benoit Mandelbrot, cha đẻ của hình học fractal.

Tập Mandelbrot đẹp tuyệt vời. Đó là một tác phẩm nghệ thuật tinh tế, được tạo ra bởi một phương trình đơn giản.

Chính thức hơn, tập Mandelbrot là tập các số phức c, trong đó phương trình z² + c không phân kỳ khi lặp lại từ z = 0.

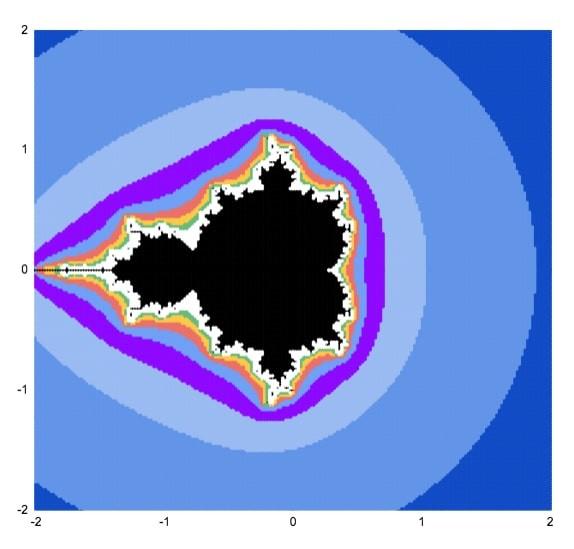
Nếu bạn vẫn chưa hình dung được, hãy quan sát thêm lần nữa bức ảnh ở trên cùng bài viết này. Vùng màu đen đại diện cho các điểm không chạy xa đến vô cùng khi bạn tiếp tục áp dụng phương trình z² + c.

Nếu c = -1. Nó lặp lại -1, 0, -1, 0, -1… mãi mãi, vì vậy nó không bao giờ thoát ra được. Nó bị ràng buộc nên nó thuộc về tập Mandelbrot.

Bây giờ hãy xem xét c = 1. Bắt đầu với z = 0, lần lặp đầu tiên là 1.

Lần lặp thứ hai là 1² + 1 = 2.

Lần lặp thứ ba là 2² + 1 = 5.

Lần lặp thứ tư là 5² + 1 = 26.

Và cứ như vậy 26, 677, 458330, 210066388901,… 

Nó phân kỳ đến vô cực, vì vậy không còn nằm trong tập Mandelbrot.

Trước khi có thể vẽ tập Mandelbrot, chúng ta cần nghĩ về các số phức.

Số ảo và số phức

Không thể vẽ tập Mandelbrot mà không có hiểu biết cơ bản về số phức. Số phức là những số có dạng a + bi trong đó i là căn bậc hai của -1.

Chúng ta có thể vẽ chúng dưới dạng tọa độ trên mặt phẳng 2 chiều, trong đó hệ số thực “a” là trục x và hệ số ảo “b” nằm trên trục y.

Sử dụng biểu đồ phân tán (Scatter Plot để) vẽ tập Mandelbrot

Lần lượt lấy từng điểm trên mặt phẳng 2 chiều này, ta kiểm tra thử xem các điểm đó có thuộc tập Mandelbrot không. Nếu có, điểm này sẽ có một màu đen. Nếu không, chúng ta sẽ dán cho nó một màu khác.

Biểu đồ phân tán scatter plot của các điểm được tô màu này là một dạng hiển thị gần đúng của tập Mandelbrot.

Khi chúng tôi tăng số lượng điểm được vẽ và số lần lặp lại, chúng ta sẽ có được các chế độ xem chi tiết hơn liên tiếp của tập Mandelbrot. Một điểm vẫn có thể <2 ở lần lặp 3 có thể rõ ràng nằm ngoài ranh giới đó bởi lần lặp 5, 7 hoặc 10.

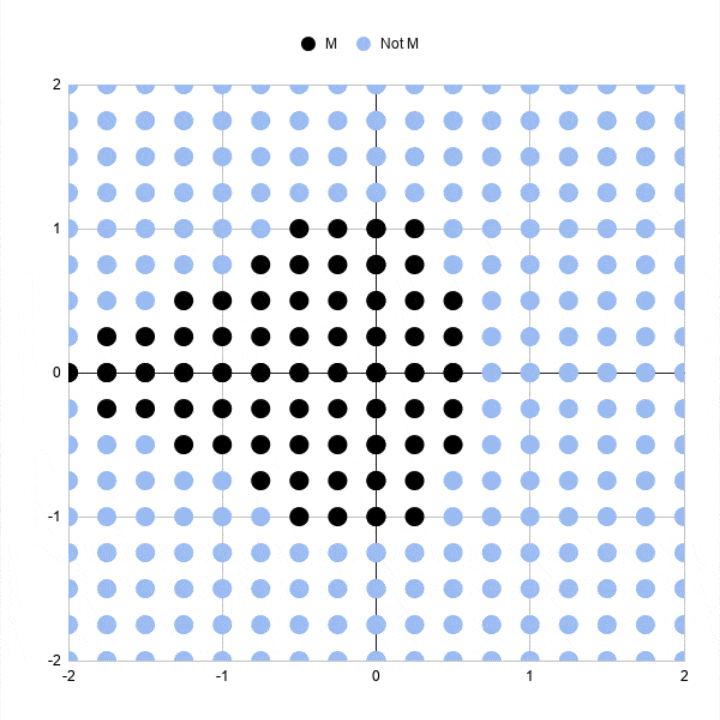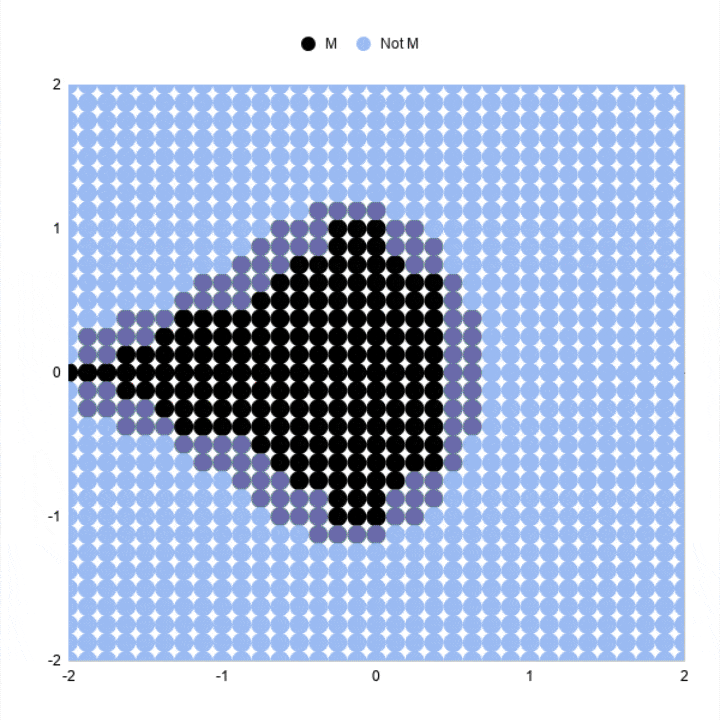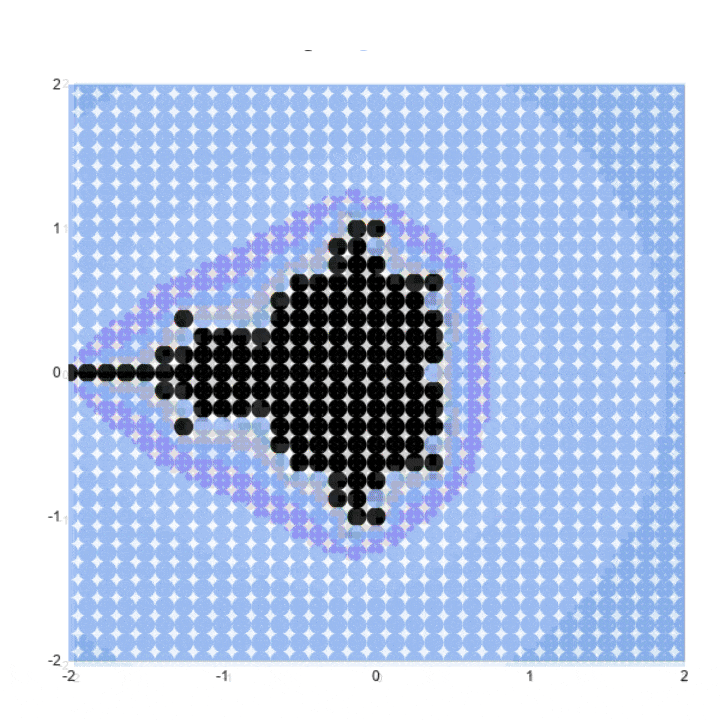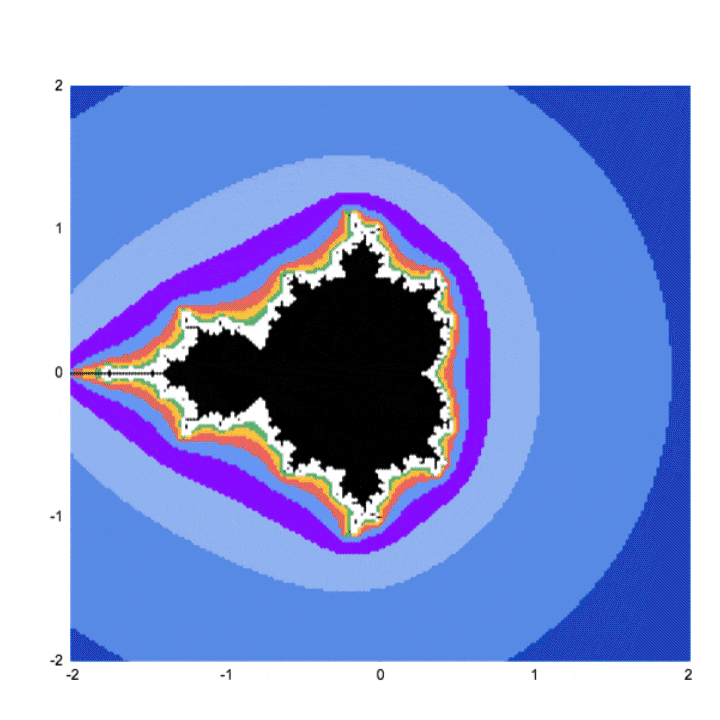
Bạn có thể thấy đường viền giống tập Mandelbrot rõ ràng hơn nhiều ở các lần lặp cao hơn.

Cách vẽ tập Mandelbrot trong Google Sheets, chỉ sử dụng công thức

Chúng tôi đã đính kèm 1 file excel ngay bên bưới để bạn có thể tải về và thực hành ngay các công thức thú vị này.

Dưới đây là một ước lượng đơn giản của tập Mandelbrot được vẽ trong Google Sheets:

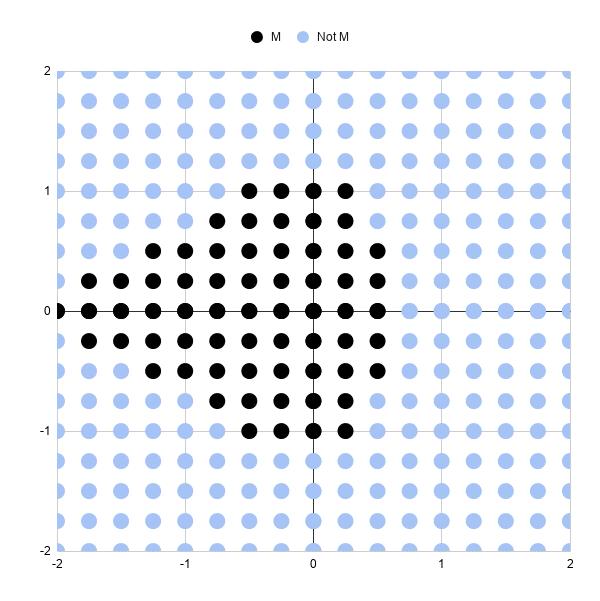
Và ngay bên dưới các bước dễ dàng để tạo nên Tập Mandelbrot này:

Thực tế đây là một bản đồ phân tán với 289 điểm (17 x 17 điểm).

Mỗi điểm được tô màu để cho biết nó có nằm trong bộ Mandlebrot hay không, sau 3 lần lặp lại.

Các điểm đen biểu thị các số phức, chỉ là các tọa độ (a, b), có kích thước vẫn nhỏ hơn hoặc bằng 2 sau 3 lần lặp. Vì vậy, chúng tôi đưa chúng vào tập Mandelbrot của mình.

Các điểm màu xanh đại diện cho các số phức có kích thước lớn hơn 2 và không có trong tập Mandelbrot của chúng ta. Nói cách khác, chúng đang phân kỳ.

Ba lần lặp lại là không nhiều, đó là lý do tại sao biểu đồ này là chỉ là một dạng rất thô sơ của tập Mandelbrot. Một số điểm đen này cùng sẽ phân kỳ nếu chúng ta cho chúng lập nhiều lần hơn nữa.

Và rõ ràng là chúng ta cần nhiều điểm hơn để có thể lấp đầy khoảng trống giữa các điểm và kiểm tra các số phức đó.

Hãy bắt đầu thôi!

Tạo tọa độ số phức

Trong cột A, chúng ta cần chuỗi từ 0 đến 2 và lặp lại {0, 0,25, 0,5, 0,75, 1, 1,25, 1,5, 1,75, 2, 0, 0,25, 0,5,…}

Trong cột B, chúng ta cần dãy 0, sau đó 0,25, rồi 0,5 lặp lại 9 lần mỗi lần cho đến khi chúng ta đạt đến 2 {0, 0, 0, 0, 0, 0, 0, 0, 0, 0,25, 0,25, 0,25,…}

Điều này cung cấp cho chúng ta các kết hợp của tọa độ x và y cho các số phức c mà chúng ta sẽ kiểm tra xem chúng có nằm trong tập hợp hay không.

Để dễ hình dung hơn, bạn hãy quan sát Sheets bên dưới:

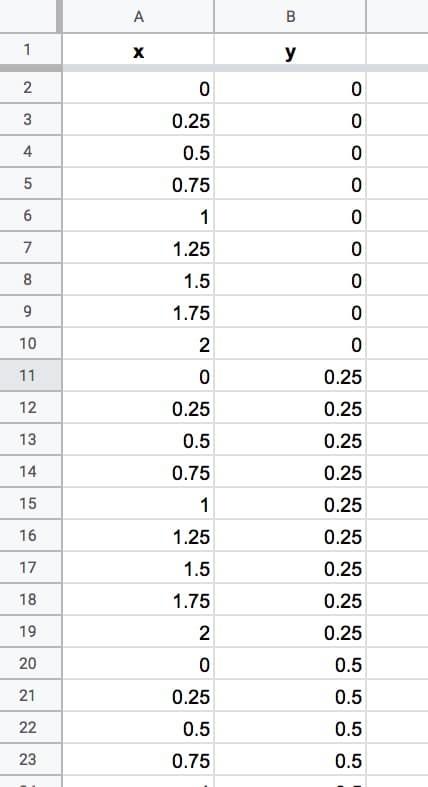
Chúng ta sẽ tiếp tục cho đến khi đạt đến số 2 trong cột B. Chúng ta có 324 hàng dữ liệu. Có một số hàng lặp lại (như 0,0) nhưng điều đó cũng không mấy quan trọng.

Các cột A và B hiện chứa các tọa độ cho lưới các số phức của chúng ta. Chúng ta không cần kiểm tra từng cái để xem nó có thuộc tập Mandelbrot không.

Công thức cho thuật toán Mandelbrot

Chúng ta sẽ tạo các bước thuật toán từ cột C đến cột J.

Trong ô C2, chúng ta tạo số phức bằng cách kết hợp các hệ số thực và ảo:

=COMPLEX(A2,B2)

Ô D2 chứa lần lặp đầu tiên của thuật toán với z = 0, vì vậy kết quả bằng C, số phức trong ô C2, do đó:

=C2

Lần lặp thứ hai nằm trong ô E2. Phương trình lần này là z² + c, trong đó z là giá trị trong ô D2 và C là giá trị từ C2:

=IMSUM(IMPOWER(D2,2),$C2)

Nó giống như z² + c trong F2, trong đó z trong trường hợp này là từ E2 (lần lặp trước):

=IMSUM(IMPOWER(E2,2),$C2)

Lưu ý dấu “$” phía trước chữ C trong cả hai công thức trong cột E và F. Điều này nhằm khóa công thức của chúng ta trở lại giá trị C cho phương trình Mandelbrot của chúng ta.

Trong ô G2:

=IMABS(D2)

Kéo công thức này qua các ô H2 và I2.

Trong ô J2:

=IFERROR(IF(I2<=2,1,2),2)

Sau đó, để lại một vài cột trống, trước khi đưa dữ liệu biểu đồ vào các cột M, N và O, với các công thức sau đại diện cho các giá trị x và hai chuỗi y với các màu khác nhau:

=A2

=IF(J2=1,B2,"")

=IF(J2=2,B2,"")

Do đó, tập dữ liệu của chúng ta bây giờ trông giống như thế này:

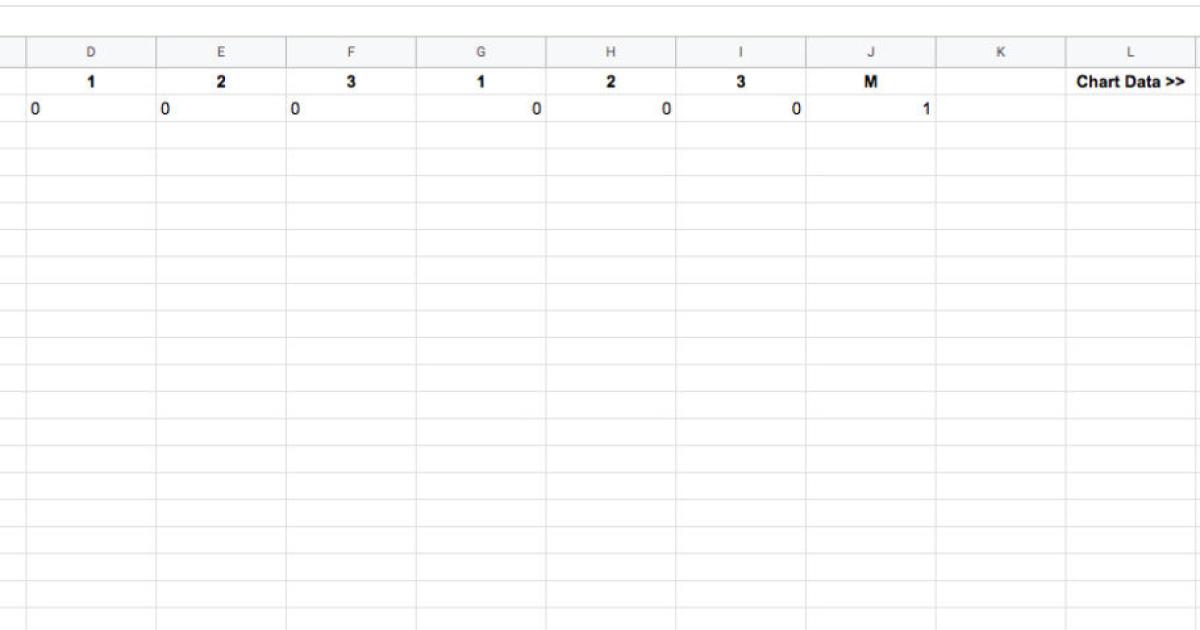
Nhiệm vụ cuối cùng là kéo hàng công thức đầu tiên xuống cuối tập dữ liệu, để mọi hàng đều được điền công thức:

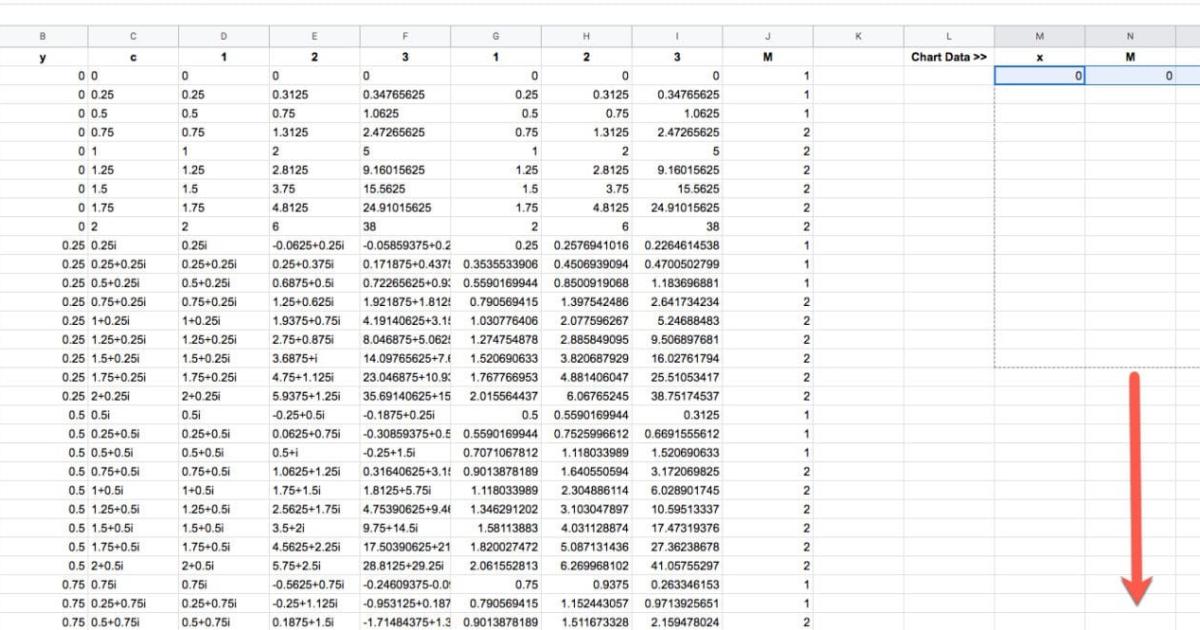
Bước chuẩn bị như vậy là đã ổn rồi, bây giờ chúng ta hãy cùng bắt đầu vẽ một hình ảnh bắt mắt nào.

Cách vẽ tập Mandelbrot trong Google Sheets

Đánh dấu các cột M, N và O trong tập dữ liệu của bạn.

Bấm Insert > Chart.

Thao tác này sẽ mở ra một Biểu đồ cột mặc định, vì vậy hãy thay đổi nó thành biểu đồ phân tán trong Setup > Chart type > Scatter chart .

Thay đổi màu sắc theo ý thích của bạn. Trong ví dụ này, tôi đã chọn màu xanh cho các số không thuộc tập Mandelbrot.

Và cuối cùng, thay đổi kích thước biểu đồ của bạn thành hình vuông, bằng cách kéo các đường viền xung quanh biểu đồ của bạn.

Kết quả thật tuyệt vời phải không?

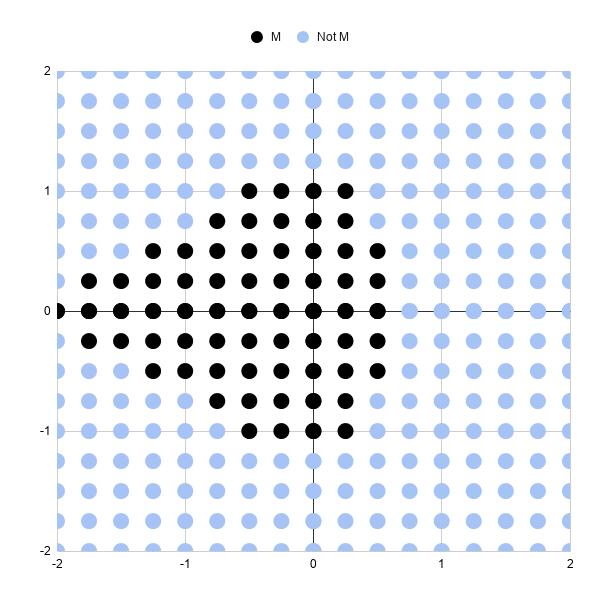
Lưu ý: bạn có thể cần đặt thủ công các giá trị tối thiểu và tối đa của trục ngang và trục dọc lần lượt là -2 và 2 trong menu tùy chỉnh Customize của trình chỉnh sửa biểu đồ.

Cách vẽ tập Mandelbrot chuyên nghiệp hơn trong Google Sheets

Tạo dữ liệu tự động

Việc tạo các tọa độ xy đó theo cách thủ công như hướng dẫn ở phần trên là vô cùng tẻ nhạt và không thực sự thiết thực ngoài ví dụ đơn giản ở trên.

May mắn thay, bạn có thể sử dụng công thức SEQUENCE tuyệt vời trong Google Sheets để trợ giúp bạn. Công thức này sẽ tạo ra các tọa độ xy cho lưới 33 x 33, lưới này mang lại nhiều hình ảnh hơn so với ví dụ đơn giản ở trên.

=ArrayFormula(UNIQUE({
MOD(SEQUENCE(289,1,0,1),17)/8,
ROUNDDOWN(SEQUENCE(289,1,0,1)/17)/8;
-MOD(SEQUENCE(289,1,0,1),17)/8,
ROUNDDOWN(SEQUENCE(289,1,0,1)/17)/8;
MOD(SEQUENCE(289,1,0,1),17)/8,
-ROUNDDOWN(SEQUENCE(289,1,0,1)/17)/8;
-MOD(SEQUENCE(289,1,0,1),17)/8,
-ROUNDDOWN(SEQUENCE(289,1,0,1)/17)/8
}))

Sau đó, kéo các công thức khác xuống các hàng của bạn để hoàn thành tập dữ liệu, giống như cách chúng ta đã làm ở trên.

Tiếp đến, bạn có thể đánh dấu các cột M, N và O để vẽ lại biểu đồ của mình.

Lưu ý: bạn có thể cần đặt thủ công các giá trị tối thiểu và tối đa của trục ngang và trục dọc lần lượt là -2 và 2 trong menu tùy chỉnh Customize của trình chỉnh sửa biểu đồ.

Với ba lần lặp lại, biểu đồ trông như sau:

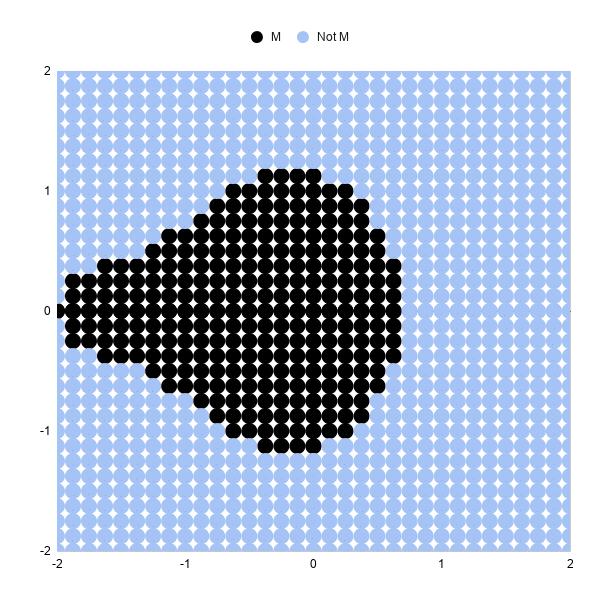
Tăng số lần lặp

Để thấy nhiều chi tiết hơn, chúng ta hãy thử tăng số lần lập lên thành 5 và 10 lần lập.

Để chuyển từ 3 lần lặp thành 5, chúng ta cần thêm một số cột vào Sheets của mình và lặp lại thuật toán hai lần nữa.

Vì vậy, hãy chèn hai cột trống giữa F và G. Dán nhãn cho các tiêu đề 4 và 5.

Kéo công thức trong F2 qua các cột trống mới G và H (đây là phương trình z² + c dưới dạng công thức Google Sheets):

Trong G2:

=IMSUM(IMPOWER(F2,2),$C2)

Trong H2:

=IMSUM(IMPOWER(G2,2),$C2)

Chúng ta cần thêm các cột tính toán kích thước tương ứng. Giữa K và L, chèn hai cột trống mới và kéo công thức IMABS qua.

Bây giờ trong L2:

=IMABS(G2)

Và trong M2:

=IMABS(H2)

Cuối cùng, cập nhật câu lệnh IF sau trong cột để đảm bảo kiểm tra giá trị trong cột M:

=IFERROR(IF(M2<=2,1,2),2)

Biểu đồ của chúng ta sẽ cập nhật và trông như thế này:

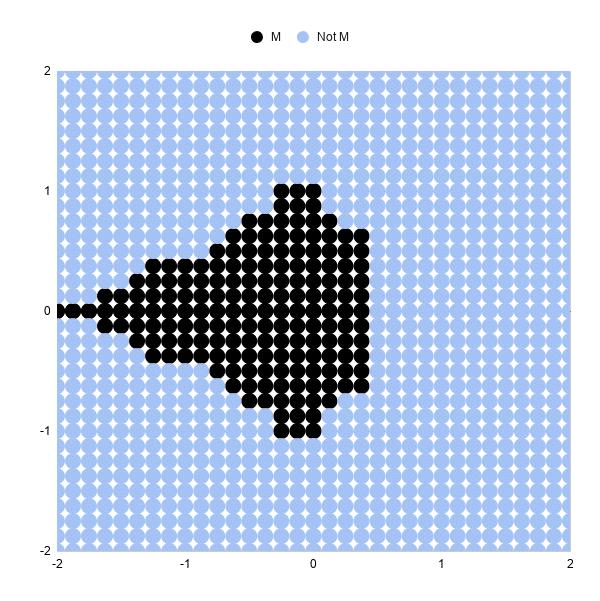
Bạn có thể thấy hình dạng của tập Mandelbrot bây giờ rõ ràng hơn nhiều.

Tăng từ 5 lần lặp lên 10 lần lặp là hoàn toàn giống nhau. Thêm 5 cột trống và điền lại các công thức.

Biểu đồ lặp lại 10 kết quả lại tốt hơn:

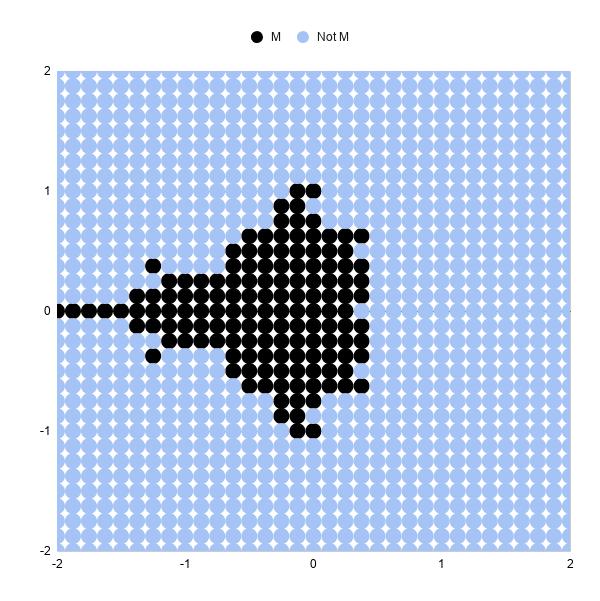
Tăng số điểm dữ liệu

Tăng số điểm lên 6,561 trong một lưới 81 x 81 sẽ cho một bức tranh "hoàn chỉnh" hơn các ví dụ trên.

Công thức trình tự này sẽ tạo ra các điểm dữ liệu sau:

=ArrayFormula(UNIQUE({
MOD(SEQUENCE(1681,1,0,1),41)/20,
ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20;
-MOD(SEQUENCE(1681,1,0,1),41)/20,
ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20;
MOD(SEQUENCE(1681,1,0,1),41)/20,
-ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20;
-MOD(SEQUENCE(1681,1,0,1),41)/20,
-ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20
}))

Lưu ý rằng khi bạn tăng số lượng công thức trong Sheets và số điểm cần vẽ trong biểu đồ phân tán, Sheets của bạn sẽ bắt đầu chậm lại!

Thêm dải màu

Chúng ta có thể thêm các dải màu để hiển thị sự lặp lại nào của một điểm đã cho "thoát" về phía vô cùng.

Ví dụ: tất cả các điểm lớn hơn ngưỡng của chúng ta ở lần lặp 5 sẽ có màu khác với những điểm nhỏ hơn ngưỡng ở lần lặp 5, nhưng trở nên lớn hơn ở lần lặp 6.

Các công thức cho các lần lặp và kích thước giống như các ví dụ ở trên.

Sau đó, chúng ta sẽ xác định xem điểm vẫn nằm trong tập Mandelbrot:

=IF(ISERROR(AG2),"No",IF(AG2<=2,"Yes","No"))

Và sau đó lần lặp nào mà nó "thoát" đến vô cùng hoặc vượt quá ngưỡng 2 trong ví dụ này:

=IF(AH2="Yes",0,MATCH(2,S2:AG2,1))

Tiếp theo, chúng tôi tạo chuỗi cho biểu đồ:

Đầu tiên, tập Mandelbrot:

=IF(AH2="Yes",B2,"")

Sau đó, chuỗi 1 đến 15:

=IF($AI2=AK$1,$B2,"")

Phạm vi cho biểu đồ phân tán sau đó là:

A1:A6562,AJ1:AY6562

trong đó cột A là các giá trị trục x và cột AJ đến AY là chuỗi trục y.

Vẽ biểu đồ phân tán và điều chỉnh màu sắc chuỗi sẽ tạo ra một bức tranh đẹp (đây là lưới 81 x 81):

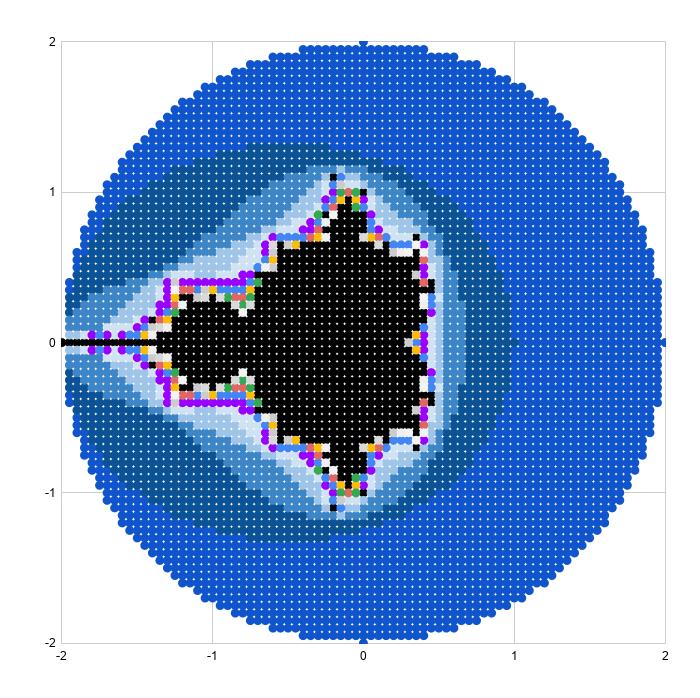
Đạt đến giới hạn thực tế của Google Sheets

Chúng tôi sẽ thử tăng kích thước ô lên 40,401 đại diện cho một lưới 201 x 201 điểm. Điều này thực sự làm chậm Sheets của bạn và mất khoảng nửa giờ để hiển thị biểu đồ phân tán, vì vậy mặc dù hình ảnh rất đẹp mắt nhưng không thích hợp để chúng ta áp dụng thực tế.

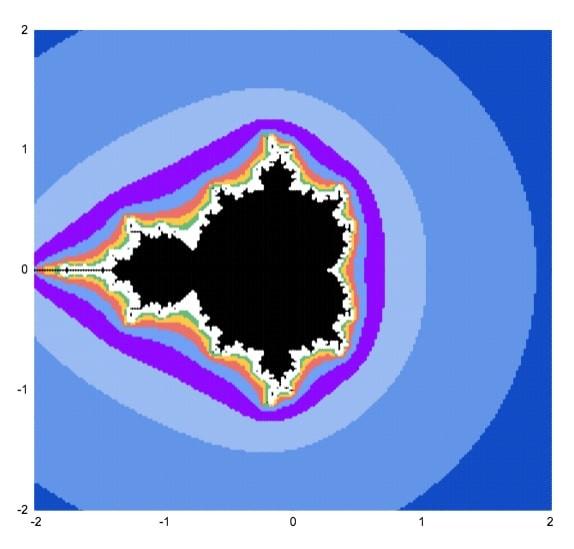
Dưới đây là cách vẽ tập Mandelbrot trong Google Sheets

Tọa độ 40,401 xy có thể được tạo bằng công thức mảng sau:

=ArrayFormula(UNIQUE({
MOD(SEQUENCE(10201,1,0,1),101)/50,
ROUNDDOWN(SEQUENCE(10201,1,0,1)/101)/50;
-MOD(SEQUENCE(10201,1,0,1),101)/50,
ROUNDDOWN(SEQUENCE(10201,1,0,1)/101)/50;
MOD(SEQUENCE(10201,1,0,1),101)/50,
-ROUNDDOWN(SEQUENCE(10201,1,0,1)/101)/50;
-MOD(SEQUENCE(10201,1,0,1),101)/50,
-ROUNDDOWN(SEQUENCE(10201,1,0,1)/101)/50
}))

Phóng to tập Mandelbrot

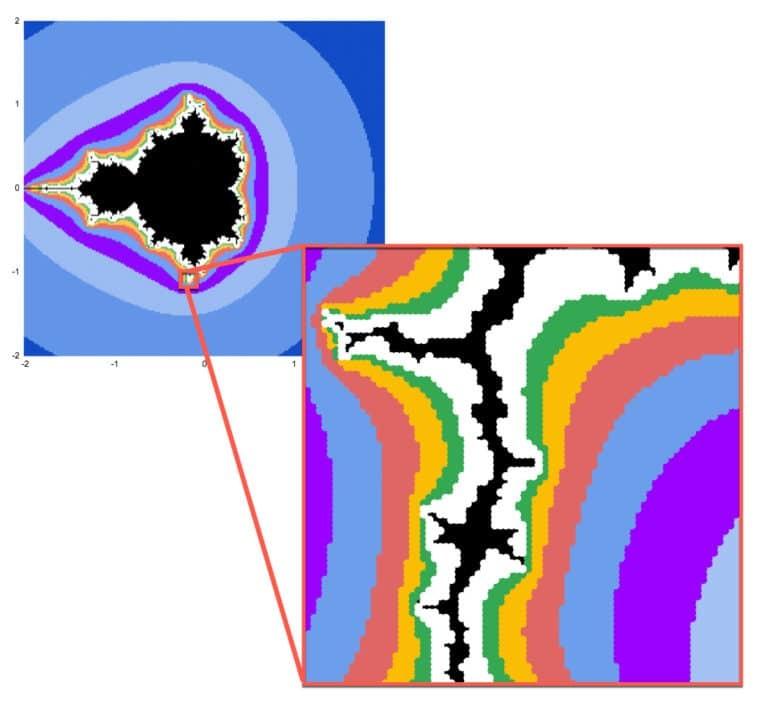
Chúng ta có thể phóng to bất kỳ phần nào của biểu đồ và xem cùng một dạng hình học fractal diễn ra trên các tỷ lệ nhỏ hơn vô hạn. Đây chỉ là một trong những đặc tính đáng kinh ngạc của tập Mandelbrot.

Google Sheets chắc chắn không phải là công cụ tốt nhất để khám phá tập Mandelbrot ở độ phân giải ngày càng tăng. Công cụ này quá chậm để kết xuất đồ họa và quá thủ công để thực hiện các thay đổi đối với công thức và giới hạn trục.

Tuy nhiên, như châm ngôn đã nói

công cụ tốt nhất là công cụ bạn phải có trong tay.

Vì vậy, nếu bạn muốn khám phá trong Google Sheets, bạn có thể thực hiện các bước hướng dẫn trong bài viết này để phục vụ nhu cầu của mình.

Cách tạo dữ liệu có thể Zoom

Chúng ta sẽ phóng to điểm: -0.17033700000, -1.06506000000

Bạn hãy bắt đầu với công thức này trong ô A2 để tạo ra 6,561 điểm dữ liệu.

=ArrayFormula(UNIQUE({
MOD(SEQUENCE(1681,1,0,1),41)/20,
ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20;
-MOD(SEQUENCE(1681,1,0,1),41)/20,
ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20;
MOD(SEQUENCE(1681,1,0,1),41)/20,
-ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20;
-MOD(SEQUENCE(1681,1,0,1),41)/20,
-ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20
}))

Trong cột C và D, chúng tôi đã chuyển đổi dữ liệu này bằng cách thay đổi tâm 0,0 thành -0.17033700000, -1.06506000000 và sau đó thêm các giá trị từ A và B vào C và D tương ứng, chia cho 100 để phóng to.

=C$2+A3/100

=D$2+B3/100

Phần còn lại của quá trình cũng tương tự như các hướng dẫn trên.

Chúng ta đặt các trục biểu đồ các giá trị tối thiểu và tối đa để khớp với các giá trị tối thiểu và tối đa trong mỗi cột C (trục x) và D (trục y).

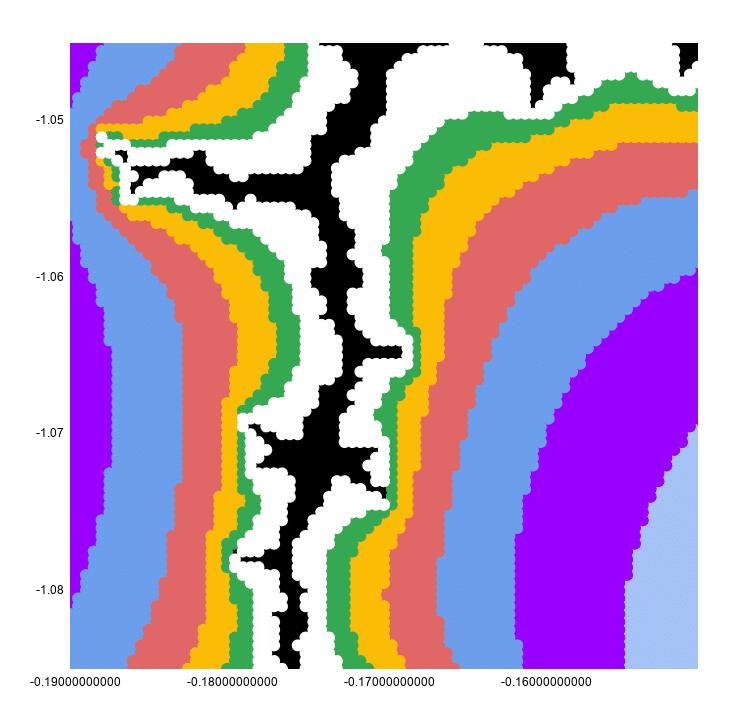
Hình này trông liên tục vì biểu đồ có kích thước điểm là 10px để làm cho nó trông đẹp hơn.

Nếu chúng ta đặt lại thành 2px, bạn có thể thấy rõ rằng đây vẫn là một biểu đồ phân tán:

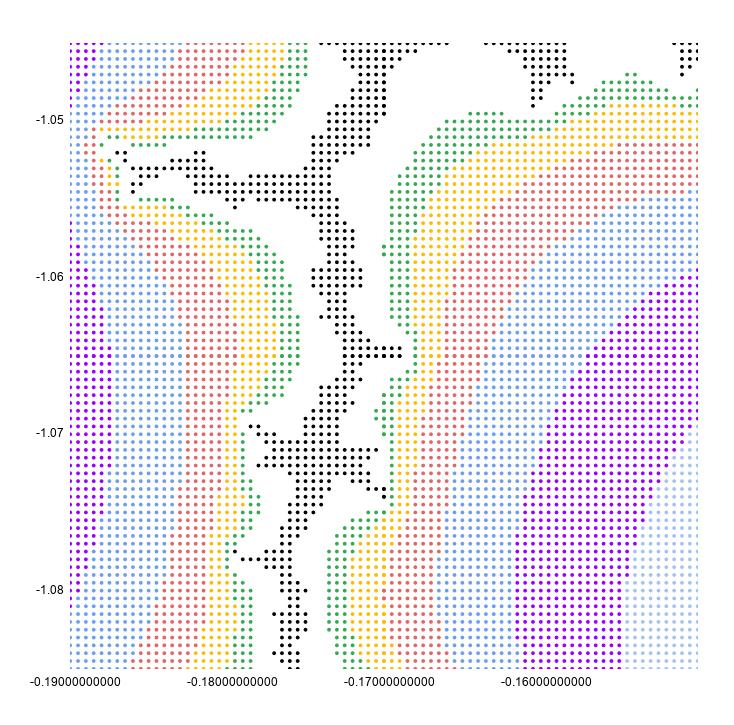
Chúng tôi hy vọng bạn thích cách vẽ tập Mandelbrot tuyệt đẹp trong Google Sheets mà chúng ta vừa khám phá trong bài viết này.

Để không bỏ lỡ các thủ thuật tin học văn phòng hữu ích khác. Hãy tham gia cùng với Gitiho ngay hôm nay.