LÃI SUẤT VÀ DÒNG TIỀN – Phân Tích Tài Chính Doanh Nghiệp Cơ bản (Phần 1)

Khi phân tích tài chính doanh nghiệp bạn phải nắm rõ các định nghĩa và phép tính về lãi suất và dòng tiền. Hãy cùng tìm hiểu qua ví dụ thực tế sau của Gitiho nhé!

Lãi suất và dòng tiền, đây là một trong những kiến thức nền tảng của tài chính doanh nghiệp. Đọc hiểu xong phần này chúng ta có thể nắm vững được các khái niệm về thời giá của tiền tệ bao gồm:

• Giá trị tương lai của một lượng tiền và của một dòng tiền.
• Giá trị hiện tại của một lượng tiền và của một dòng tiền.
• Tìm được lãi suất, thời gian đầu tư các các khoản vay hay đầu tư.

Giá trị tương lai của một lượng tiền có nghĩa là ta bỏ ra một khoản tiền, trong tương lai nó sẽ là bao nhiêu. 

Giá trị tương lai của một dòng tiền có nghĩa là chúng ta có các khoản chi phí, khoản thu nhập liên tiếp nhau, xảy ra trong một khoảng thời gian liên tục. Tạo ra một khoản giá trị tương lai, thì giá trị đó như thế nào.

Tương tự vậy chúng ta cũng nghiên cứu về giá trí hiện tại của một lượng tiền và của một dòng tiền.

Đồng thời mục tiêu của bài cũng giúp chúng ta nắm được rõ ràng mô hình Chiết Khấu dòng tiền DCF và ứng dụng của nó trong phân tích tài chính doanh nghiệp hay kinh doanh chứng khoán.

Và tất nhiên chúng ta cũng tìm hiểu về việc sử dụng ứng dụng MS Excel để giải các bài toán về thời giá tiền tệ.

Các loại lãi suất cần biết khi phân tích tài chính doanh nghiệp

Chúng ta lấy ví dụ tình huống cụ thể luôn như sau: 

Giả sử bây giờ bạn bỏ ra số tiền là 10 triệu đồng để gửi ngân hàng, với kỳ hạn 1 năm, lãi suất là 10%/năm.

Sau 01 năm bạn sẽ nhận được số tiền là bao nhiêu?

Sau 05 năm bạn sẽ nhận được số tiền là bao nhiêu?

Số tiền chúng ta nhận được sẽ gồm cả gốc và lãi.  

Sau 1 năm chúng ta nhận lại = 10tr + 10tr x 10% = 11tr

Sau 5 năm chúng ta nhận lại = 10tr x (1+10%)5 = 16.1 tr

Đây là cách tính lãi đơn và lãi kép .

Xem thêm: Cách sử dụng hàm RATE, hàm tính lãi suất trong Excel

Lãi suất là gì?

Là lợi tức trong một đơn vị thời gian chia cho vốn gốc, tính theo phần trăm. Trong một đơn vị thời gian nghĩa là dùng đơn vị thời gian là năm thi ta gọi là lãi suất năm, tính theo tháng là lãi suất tháng, tính theo ngày là lãi suất ngày.

Lãi suất (%) = Lợi tức trong 1 đơn vị thời gianVốn gốcx 100%

Đối với người cho vay: Lãi suất chính là suất thu lợi tức, là tỷ lệ phần trăm (%) của giá trị thu được do việc cho vay vốn mang lại so với giá trị cho vay ban đầu.

Đối với người đi vay: Lãi suất chính là suất thu lợi tức do hoạt động sản xuất, kinh doanh mang lại hay là chi phí phải trả cho việc sử dụng vốn vay.

Đối với người tiêu dùng: Là phần thưởng cho người tiêu dùng vì họ đã hoãn việc tiêu thụ của mình để dành cho dịp khác trong tương lại.

Ví dụ ta gửi 10 triệu sau 1 tháng ta thu được lãi 100 nghìn đồng. Vậy lãi suất này là lãi suất tháng, ta tính được:

Lãi suất (%) = 100.000 / 10.000.000 x 100 = 1 %

Lãi suất tháng lúc này là 1%.

Ví dụ như mình kinh doanh chứng khoán thì lãi suất cũng là lợi tức, là tỷ suất sinh lợi của khoản đầu tư.

Xem thêm: Hướng dẫn cách phân tích báo cáo tài chính hiệu quả

Lãi đơn

Là số tiền lãi chỉ tính trên số tiền gốc mà không tính trên số tiền lãi do gốc đó sinh ra. Công thức tính lãi đơn cụ thể như sau:

SI = PV.i.n

Trong đó:

• SI:  lãi đơn vào cuối kỳ hạn
• PV: số vốn gốc
• i: lãi suất một kỳ hạn
• n: số kỳ hạn tính lãi (theo năm, theo ngày, theo tháng)

Lãi đơn ứng dụng nhiều trong lãi trái phiếu, lãi cho vay, tín phiếu. 

Số tiền nhận được sau n kỳ hạn theo lãi đơn là:

FV = PV + Sin = PV + PV x i x n = PV(1+i x n)Ví dụ một người đầu tư vào 1 trái phiếu có mệnh giá 100 triệu đồng với lãi suất 10%/ năm trong vòng 5 năm. Hỏi sau 5 năm người đó có được bao nhiêu tiền.

Giải đáp: Trong trường hợp cần tính lãi của trái phiếu chúng ta áp dụng công thức tính lãi đơn:

• Sau 5 năm số tiền lãi người đó thu được là: 100 x 10% x 5 = 50 triệu
• Tổng số tiền gốc và lãi người đó thu được là: 100 x (1+10% x 5) = 150 triệu đồng

Xem thêm: HƯỚNG DẪN CÁCH SỬ DỤNG HÀM TÍNH LÃI SUẤT TRONG EXCEL

Lãi kép

Lãi kép là số tiền lãi không chỉ tính trên số tiền gốc mà còn tính trên số tiền lãi do số tiền gốc đó sinh ra.

Lãi kép áp dụng tính trong tiền gửi ngân hàng, tính giá trị tiền tệ theo thời gian của các khoản đầu tư (cổ phiếu, lãi suất trái phiếu tái đầu tư,…)

Nếu ta xem xét vốn đầu tư ban đầu là PV đầu tư trong vòng n kỳ hạn với lãi suất mỗi kỳ là i, gọi FVn là số tiền sau n kỳ, ta sẽ có:

FV1 = PV + PV x i = PV(1+i)

Nếu ta xem xét vốn đầu tư ban đầu là PV đầu tư trong vòng n kỳ hạn với lãi suất mỗi kỳ gọi là i, gọi FVn là số tiền sau n kỳ, ta sẽ có:

FV1 = PV + PV x i = PV(1+i)Lãi được nhập gốc để tính lãi cho kỳ sau, đến cuối kỳ thứ hai ta sẽ có:

FV2 = FV1 + FV1 x i = FV1(1+i) = PV(1+i)2Một cách tổng quát ta có:

FV5 = PV(1 + i)5FVn = PV(1 + i)nĐây là cách tính lãi kép, rất đơn giản phải không nào?

Chúng ta cùng thực hành ví dụ sau:

 Một người gửi ngân hàng 10 triệu đồng vào tài khoản định kỳ tính lãi kép với lãi suất 8%/năm.

Hỏi sau 10 năm người đó nhận được bao nhiêu tiền.

Giải quyết: Số tiền người đó nhận được sau 10 năm là:

10 x (1+0.08)10 = 21.589 triệu đồng

Từ đây chúng ta có mô hình so sánh giữa lãi đơn và lãi kép: 

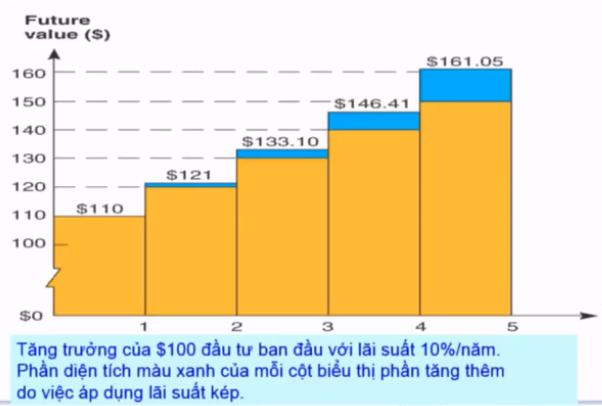
Nếu chúng ta tính theo lãi đơn thì chúng ta chỉ nhận được giá trị màu vàng thôi. Có nghĩa là chúng ta đầu tư 100 đô và mỗi năm chúng ta có lãi suất 10%. Năm thứ nhất chúng ta nhận được 110 đô. Năm thứ hai là 120 đô. Năm thứ ba là 130 đô. Năm thứ tư là 140 đô. Năm thứ năm là 150 đô.

Nhưng nếu chúng ta tính lãi kép. Năm thứ nhất chúng ta vẫn chỉ nhận 110 đô. Nhưng năm thứ 2 chúng ta đã nhận thêm được 1 đô, tổng thành 121 đô. Năm thứ 3 chúng ta nhận được 3.21 đô sinh ra, vậy là có 133.1 đô. Cứ như vậy chúng ta lời ra phần màu xanh nhiều hơn. 

Rõ ràng nếu chúng ta tính theo lãi kép thì sẽ lời hơn rất nhiều. 

Ví dụ khác: Hiện nay bạn có 1 khoản tiền 10 triệu đồng, sau 3 năm nữa, sau khi ra trường bạn mới cần dùng đến. Hiện tại ngân hàng đang có các loại hình gửi tiết kiệm như sau:

• 1 tháng, lãi suất 14%/năm
• 3 tháng, lãi suất 14 %/năm
• 6 tháng, lãi suất 14 %/năm
• 9 tháng, lãi suất 14 %/năm

Bạn sẽ gửi loại tiết kiệm nào?

Giải:

Trường hợp: kỳ hạn 3 tháng, lãi suất 14%/năm.

• Ta có lãi suất 1 kỳ: ikỳ = i năm12x thời hạn 1 kỳ.
• i3 tháng = 14%12×3= 3.5%.
• Ta có số kỳ đầu tư (n) = số năm x 12thời hạn 1 kỳ.
• n = 3 x 123= 12.
• FV12 = 10 triệu x (1 + 14%12x 3)12 = 15.11 triệu.

Chúng ta thấy gửi thời hạn kỳ hạn 1 tháng được nhiều tiền lời hơn so với kỳ hạn 3 tháng. Do vậy gửi thời gian ngắn nhất mang đến lãi suất cao hơn. 

Xem thêm: Phân tích Cấu trúc tài chính - Đánh giá cơ cấu Tài sản trong Báo cáo tài chính doanh nghiệp

Dòng tiền trong phân tích tài chính doanh nghiệp là gì?

Dòng tiền hay còn gọi là ngân lưu (Cash Flow) là một chuỗi các khoản thu nhập hoặc chi trả (CFt) xảy ra qua một thời kỳ nhất định.

Nghĩa là nó không phải một khoản 100 triệu hay một khoản 5 triệu, mà nó định kỳ mỗi năm hay mỗi tháng 5 triệu, 5 triệu, 5 triệu. Người ta gọi là một chuỗi khoản thu nhập, hay một chuỗi khoản chi trả. 

Ví dụ đơn giản nhất mà bạn có thể thấy là tiền thuê nhà hàng tháng. Mỗi tháng bạn thuê nhà là 2 triệu và phải trả trong vòng 1 năm. Nghĩa là trong năm đó bạn có 12 khoản phát sinh, mỗi khoản 2 triệu. Đối với các bạn đi thuê nhà, đây là một khoản chi ra. Còn đối với chủ nhà thì đây là một khoản thu nhập. Nếu chủ nhà có một khoản lương là 3 triệu. Vậy mỗi tháng chủ nhà có thu nhập 5 triệu, vậy 5 triệu đó người ta gọi là khoản tiền ròng.

• Dòng tiền bao gồm các khoản thu nhập người ta gọi là dòng tiền vào (inflows)
• Dòng tiền bao gồm các khoản chi phí người ta gọi là dòng tiền ra (outflows)
• Hiệu số giữa dòng tiền vào và dòng tiền ra người ta gọi là dòng tiền ròng (net cash flow)

Để dễ hình dung người ta thường vẽ đường biểu đồ dòng tiền như sau:

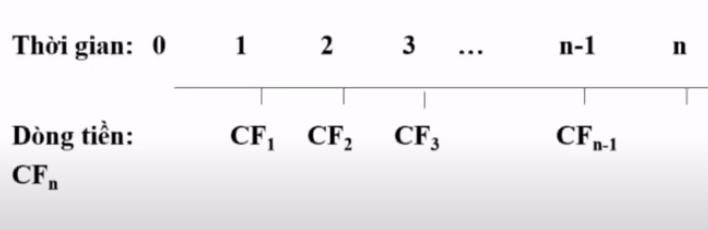
Các khoản phát sinh theo thời gian ta gọi là CFn, như vậy ta có CF1 CF2 CF3 CFn-1  toàn bộ các CF này là một dòng tiền.

Ví dụ dễ hiểu, đơn giản hơn nữa:

Ông A quyết định hàng tháng sẽ trích 1 triệu đồng từ tiền lương hưu của mình để gửi tiết kiệm vào cuối mỗi tháng, trong vòng 5 năm, ta có thể biểu diễn như sau:

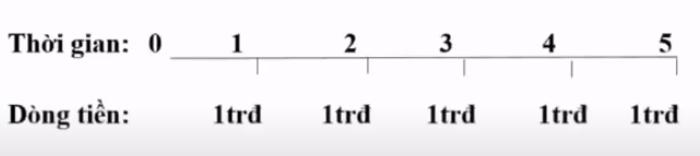
Vì khoản tiền đầu tiên ông gửi vào cuối tháng, nên khoản đầu tiền phát sinh sẽ ghi vào điểm 1.

Ghi chú: Thời điểm 0 là hiện tại, là đầu kỳ 1

Thời điểm 1 là cuối kỳ 1 đầu kỳ 2

Thời điểm 2 là cuối kỳ 2 đầu kỳ 3

Thời điểm n-1 là đầu kỳ n, và thời điểm n là cuối kỳ n.

Xem thêm: Phân tích Cấu trúc tài chính - Đánh giá cơ cấu Nguồn vốn trong Báo cáo tài chính doanh nghiệp

Kết luận

Qua bài viết này, chắc hẳn các bạn đã nắm được kiến thức cơ bản về lãi suất và dòng tiền khi phân tích tài chính doanh nghiệp. Để học thêm nhiều kiến thức về tài chính doanh nghiệp hơn, các bạn hãy tham gia vào khóa học dưới đây:

FMA01 - Phân tích Báo cáo Tài chính và Xây dựng Mô hình Tài chính cho Nhà quản lý Doanh nghiệp

Khóa học được xây dựng theo lộ trình bài bản, chuyên nghiệp vừa học lý thuyết vừa làm bài tập dựa trên case study thực tế. Kiến thức trong khóa học mang tính ứng dụng cao, bạn có thể áp dụng vào công việc hàng ngày ngay sau khi học. Hoàn thành khóa học bạn sẽ biết xây dựng kế hoạch kinh doanh, kế hoạch tài chính, mô hình tài chính, phân tích doanh nghiệp dưới góc nhìn tài chính và đánh giá được các rủi ro trong kinh doanh.

Tham gia khóa học, bạn sẽ được chuyên gia tài chính hỗ trợ trả lời mọi câu hỏi trong vòng 24h liên quan đến kiến thức trong bài học. Gitiho sẽ không giới hạn thời gian hay số lượt học nên có thể thoải mái sắp xếp lịch trình phù hợp với bản thân nhé. Chúc các bạn thành công!